Kodeclik Blog

Studying the Chinese Remainder Theorem with Python

The Chinese Remainder Theorem (CRT) is a fundamental mathematical principle that can help solve certain types of math problems. It dates back to the 3rd-5th century CE and was first documented by the Chinese mathematician Sunzi.

To understand the chinese remainder theorem, we first need to understand the concept of two integers being coprime. Note that “coprime” is different from “prime”. Being prime is a property of an integer (it is either prime or not prime). Being “coprime” is a property of two integers (two integers are either coprime or not).

Now let us define coprime carefully! Two integers are coprime (also called relatively prime or mutually prime) when they share no common factors except for 1. This means their greatest common divisor (GCD) equals 1.

For instance, 7 and 20 are coprime even though 20 is not a prime. 7’s factors are 1 and 7. 20’s factors are 1, 2, 4, 5, 10, 20. Now look at the common factors and you will see there are no common factors other than 1.

Of course, two prime numbers are also coprime. For instance, 2 and 3 are coprime because their only common factor is 1.

Finally, 6 and 9 are not coprime because 3 divides both numbers.

Bezout’s Identity

Two integers a and b are coprime if and only if there exist integers x and y such that ax+by=1.This is known as Bézout's identity.

Example 1: 7 and 20 (Coprime)

Let's find integers x and y such that 7x+20y=1. If you try x=3 and y=-1, then 7x+20y = 7(3) + 20(-1) = 21-20 = 1. Since we found values for x and y that work, this confirms that 7 and 20 are coprime.

Example 2: 8 and 9 (Coprime)

For these numbers, we need x and y where 8x+9y=1. We can find x=-1 and y=1, to get 8(-1) + 9(1) = 1. Thus 8 and 9 are coprime.

Example 3: 6 and 9 (Not Coprime)

Let's try to find x and y where 6x+9y=1. This is impossible because 6 and 9 share a common factor of 3, and so any combination of 6x + 9y will always be divisible by 3. Therefore, it's impossible to get 1 (which isn't divisible by 3). The best we can do is 6x+9y=3.

Python program to test Bezout’s Identity

Here is a Python program to explore Bezout’s identity:

def bezout_identity(a, b):
    if b == 0:
        return a, 1, 0
    gcd, x1, y1 = bezout_identity(b, a % b)
    x = y1
    y = x1 - (a // b) * y1
    return gcd, x, y

# Test our examples
examples = [(7, 20), (8, 9), (6, 9)]

for a, b in examples:
    gcd, x, y = bezout_identity(a, b)
    print(f"\n{a} and {b}:")
    print(f"GCD = {gcd}")
    print(f"{a}({x}) + {b}({y}) = {a*x + b*y}")

The bezout_identity function implements the extended Euclidean algorithm through recursive calls. Starting with two numbers a and b, it recursively divides a by b and keeps track of the quotient and remainder until it reaches a base case where b becomes 0. At this point, it has found the greatest common divisor (GCD) and begins unwinding the recursion, calculating coefficients x and y at each step that satisfy Bézout's identity.

The testing code then demonstrates this algorithm with our three example pairs: (7,20), (8,9), and (6,9). For each pair, it calls bezout_identity and prints the GCD along with the values of x and y that satisfy the equation ax + by = gcd. When the GCD is 1, this proves the numbers are coprime and provides the exact coefficients needed for Bézout's identity. When the GCD is greater than 1 (as with 6 and 9), it shows why it's impossible to find integers x and y that would sum to 1, since all linear combinations of these numbers must be divisible by their common factor.

The output will be:

7 and 20:
GCD = 1
7(3) + 20(-1) = 1

8 and 9:
GCD = 1
8(-1) + 9(1) = 1

6 and 9:
GCD = 3
6(-1) + 9(1) = 3

Geometric Interpretation of Coprimality

A fascinating geometric interpretation exists: two numbers a and b are coprime if and only if a point with coordinates (a,b) would be visible from the origin (0,0) without any integer coordinate points blocking the view.

Lets use Desmos to draw a line from (0,0) to (7,20).

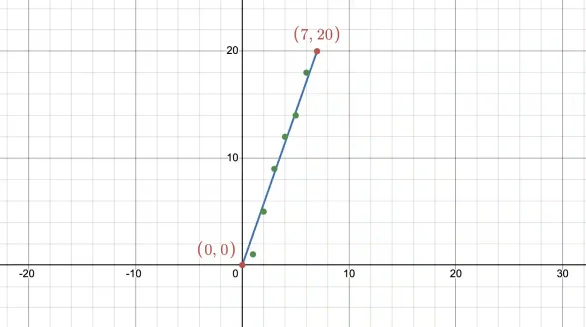
Let's prove why the point (7,20) is visible from the origin by examining the line segment between (0,0) and (7,20).

The line connecting (0,0) to (7,20) has a slope of 20/7 ≈ 2.857142857142857. For any potential point (x,y) on this line segment:

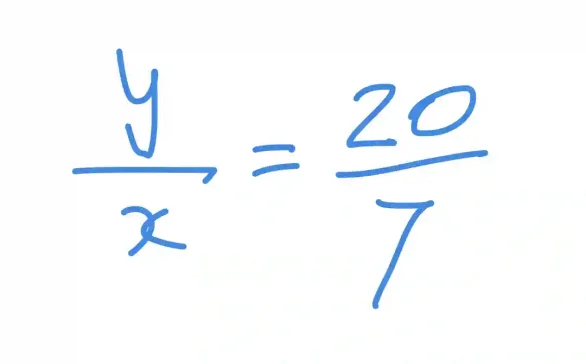
For any point (x,y) to be a blocking integer point, it must be the case that x and y are integers, and there must exist some k where 0 < k < 1 such that x=7k and y=20k. Since 7 and 20 are coprime, no value of k (except 0 and 1) can satisfy these conditions. Therefore, (7,20) is visible from the origin, confirming that 7 and 20 are coprime.

This geometric interpretation of coprime numbers is elegant and can be understood through the concept of lattice points and line segments. When we draw a line from (0,0) to point (a,b), this line is "blocked" if there exists any point with integer coordinates lying on it. For a point to have integer coordinates and lie on this line, it must be of the form (ka, kb) where k is some fraction between 0 and 1.

What does the Chinese Remainder Theorem Say?

Now that we understand what coprime means, we are ready to undertake the chinese remainder theorem.

The Chinese remainder theorem states that if we know the remainders when dividing a number by several coprime integers (numbers that share no common factors except 1), we can uniquely determine the number up to the product of those divisors.

Wow - that is a mouthful! Let us unpack that with an example.

Assume we are asked to find a number that when divided by 3 gives remainder of 2, when divided by 5 gives remainder of 3, and when divided by 7 gives a remainder of 2.

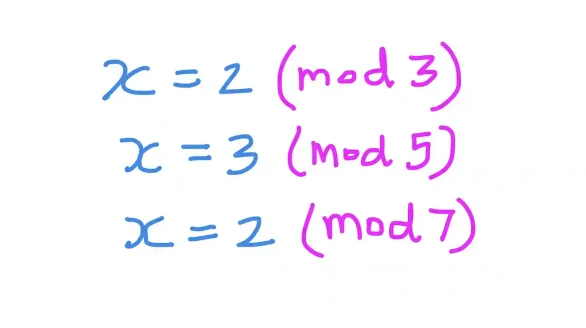
We can write this mathematically as:

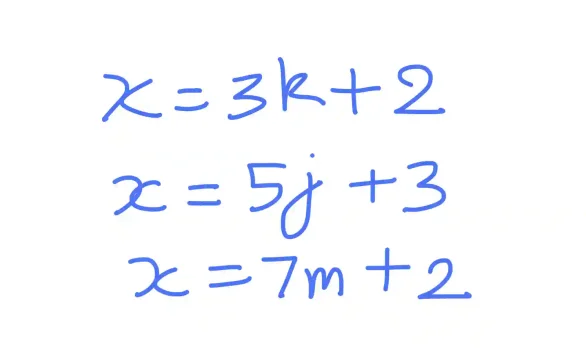
Our number must fit all three equations at once. This means the expressions must be equal to each other:

Here's how we can solve this. Let us first try to find numbers that satisfy the first condition, i.e., when divided by 3 give a remainder of 2. Such numbers start with 2 (the desired remainder) and keep adding the divisor (3). So for instance answers can be 2, 5, 8, …

Now from this list, let us filter out to find numbers that satisfy the second condition, i.e., when divided by 5 should give a remainder of 3. Such numbers will have the form 3, 8, 13, .. Hey - 8 is in common between these two lists! So 8 is a number that satisfies the two. After 8, we can find more numbers by adding the LCM of 3 and 5, ie 15. So that would be 8, 23, 38, and so on.

Finally, let us apply the third condition. This condition states that when divided by 7 we should get a remainder of 2. We immediately see that the second number satisfies it for us, which is 23. Thus 23 is the smallest number that satisfies these conditions.

But notice that it is not the only number. You can keep adding multiples of the LCM of 3, 5, and 7, which is 105. Thus the next number is 23+105=128, and so on.

Python program to explore the Chinese remainder theorem

Here's a Python program to solve Chinese Remainder Theorem problems:

def extended_gcd(a, b):
    if a == 0:
        return b, 0, 1
    gcd, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return gcd, x, y

def chinese_remainder_theorem(congruences):
    # Extract divisors and remainders from tuples
    num = [n for n, r in congruences]
    rem = [r for n, r in congruences]
    
    # Compute product of all numbers
    prod = 1
    for n in num:
        prod *= n
    
    result = 0
    # Apply CRT formula
    for n, r in zip(num, rem):
        pp = prod // n
        gcd, inv, _ = extended_gcd(pp, n)
        result += r * pp * inv
    
    return result % prod

# Example usage
congruences = [(3, 2), (5, 3), (7, 2)]
solution = chinese_remainder_theorem(congruences)
print(f"The solution is: {solution}")

The program takes a list of tuples where each tuple contains two numbers: the divisor and the remainder. For example, (3, 2) means when divided by 3, the remainder is 2. The list of tuples [(3, 2), (5, 3), (7, 2)] is basically the problem above that we solved by hand.

The extended_gcd function implements the extended Euclidean algorithm to find multiplicative inverses, while the chinese_remainder_theorem function combines these results using the CRT formula to find the unique solution.

For the above inputs, we will get the output:

The solution is: 23

The Chinese Remainder Theorem plays several crucial roles in modern cryptography and computer security. Explore it with your own number choices in the above Python programs!

Enjoy this blogpost? Want to learn Python with us? Sign up for 1:1 or small group classes.