Kodeclik Blog
Calculating the missing length of a triangle
Triangles are among the most fundamental shapes in geometry, and finding a missing side is one of the most common problems you’ll face. The method you use depends on the type of triangle and what information you already know — sides, angles, or both. Let’s go step by step through the main cases.
Calculating the missing length of a right triangle
A right triangle is one that has a 90 degree angle. Note that a triangle can have at most one 90 degree angle (why?). This is because all three angles have to add upto 180 degrees and if two angles add upto 180 degrees already, then the third will have to be zero, which is impossible.
For right triangles, the Pythagorean theorem is your best friend. It can be understood w.r.t. the following figure:
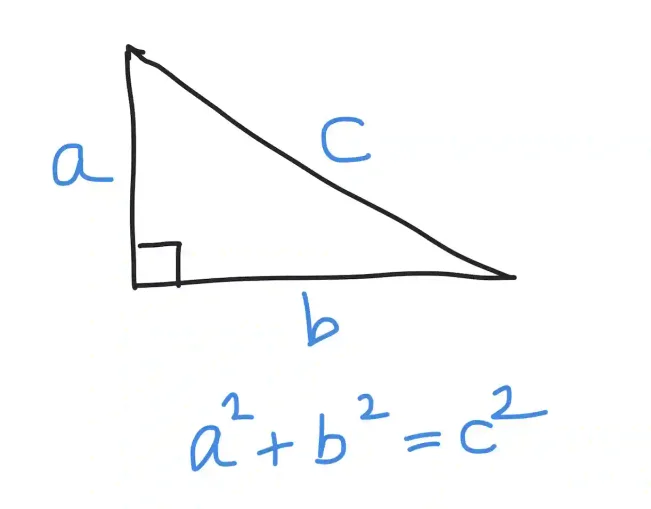
where a and b are the legs and c is the hypotenuse (the side opposite the right angle).
For instance, if you have two sides 5 and 12 and these are the legs, then the hypotenuse will be:
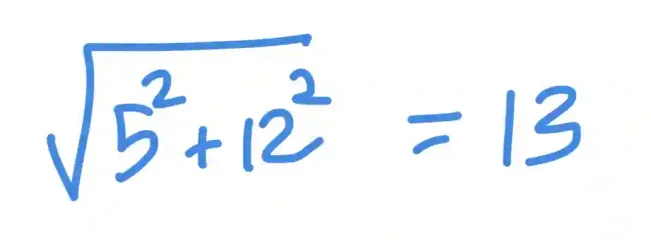
On the other hand, if 12 is the hypotenuse, the other missing leg will be:
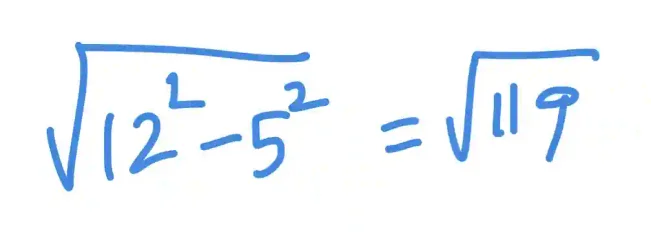
The Pythagorean theorem works for all kinds of right triangles. However, some have special, predictable ratios between their sides and angles, which makes it much easier to calculate the missing side without using the full Pythagorean theorem every time.
The two most common special cases are the 30-60-90 triangle and the 45-45-90 triangle. These appear often in geometry problems, trigonometry, and even real-world design because their ratios are simple and consistent.
Calculating the missing length of a 30-60-90 triangle
A 30-60-90 triangle is a right triangle with one angle of 30°, one of 60°, and one of 90°. The sides of such a triangle always follow the fixed ratio 1 : √3 : 2. The shortest side — the one opposite the 30° angle — acts as the base reference for the rest of the triangle.
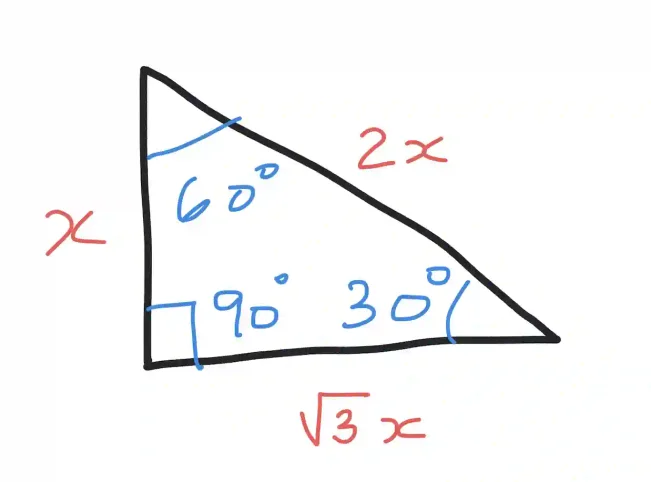
If this side has length x, then the longer leg (opposite the 60° angle) will always measure x√3, and the hypotenuse (opposite the right angle) will be 2x.
This ratio means that you only need to know one side (plus the fact that it is a 30-60-90 triangle) to find the other two by simple multiplication or division. For example, if the shorter leg of a 30-60-90 triangle is 5 cm, then the hypotenuse must be 10 cm, and the longer leg must be 5√3≈8.665 cm. No matter how large or small the triangle, these proportions stay constant, so it’s easy to scale them up or down.
Calculating the missing length of a 45-45-90 triangle
A 45-45-90 triangle is another special right triangle, but this one is also isosceles, meaning the two legs are equal in length. Because both acute angles are 45°, the ratio of the sides is always 1 : 1 : √2. The equal legs lie opposite the 45° angles, and the hypotenuse (opposite the right angle) is always the length of a leg multiplied by √2.
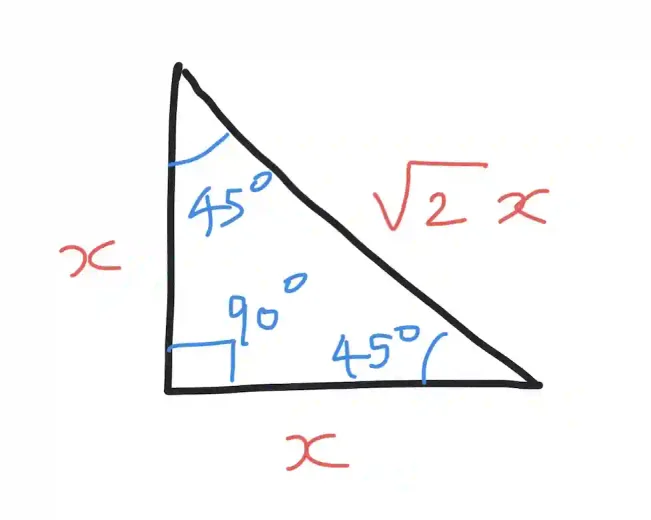
For instance, if one leg of a 45-45-90 triangle measures 7 units, the other leg is also 7 units, and the hypotenuse will be 7√2≈9.9 units. This predictable ratio saves time and avoids messy algebra — once you recognize the triangle as 45-45-90, finding the missing side is a matter of applying the √2 rule.
What is the Triangle Is Not Right?
When a triangle doesn’t have a 90° angle, the Pythagorean theorem no longer applies directly. In these cases, finding a missing side requires trigonometry, which uses relationships between sides and angles in any kind of triangle. Two main tools handle this: the Law of Sines and the Law of Cosines. These formulas let you connect sides and angles even when the triangle is scalene (no equal sides) or obtuse (one angle greater than 90°).
Law of Sines
The Law of Sines is most useful when you know one side and two angles (or sometimes two sides and a non-included angle). It states that the ratio of a side to the sine of its opposite angle is the same for all three sides of the triangle:
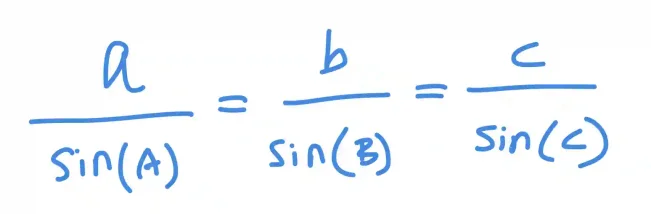
This allows you to find a missing side if you know one side and the corresponding angles. For instance, if you know that side a=10 and angle A=40°, and another angle B=70°, you can first find the third angle C=70° (since all angles add to 180°) and then solve for the other sides using the sine ratio.
Sometimes, you might know two sides but not the angle between them. In that case, the Law of Sines can still help, but it introduces what’s known as the ambiguous case — there may be one, two, or even no possible triangles that fit the given information. This happens because the same sine value can correspond to two different angles (e.g., sin(40°) = sin(140°)).
Law of Cosines
The Law of Cosines, on the other hand, comes into play when you know two sides and the included angle (the angle between those sides). It’s a generalization of the Pythagorean theorem and looks like this:
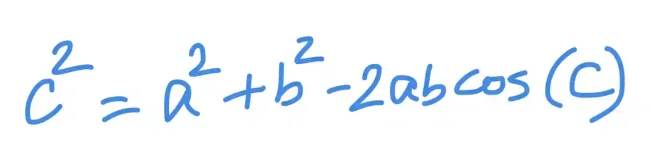
This formula works for any triangle — right, acute, or obtuse — and allows you to calculate the third side directly. For example, if a=5, b=7, and C=60°, then c=square root of (5^2 + 7^2 - 2×5×7×\cos(60°) which is 6.29.
In short, when the triangle isn’t right-angled, you’ll need to move beyond simple square roots and ratios. Trigonometry provides the tools, but it also requires careful attention to which sides and angles you’re working with — and whether more than one triangle might satisfy the same data.
Calculating the missing length from two side and an angle
When you know two sides and the included angle of a triangle (often called the SAS case), you can use the Law of Cosines to find the missing third side. As stated above, this law extends the Pythagorean theorem to work for any triangle — whether acute, obtuse, or right — and directly relates all three sides to one of the angles.
The formula is as before:
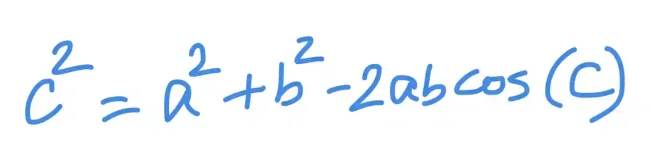
Here, C is the angle between sides a and b, and c is the side opposite that angle. Once you substitute the known values, you take the square root to find c.
For example, if a=6, b=9, and C=50°, then: c=62+92−2×6×9×cos(50°)≈7.0.
This method works for any triangle and gives a precise answer for the missing side.
Calculating the missing length given one side and two angles
If you know one side and two angles (the ASA or AAS case), the Law of Sines is the simplest approach. Start by finding the third angle, since all three angles in a triangle add up to 180°. Then, use the known side and its opposite angle to calculate the others. Again, we can use the Law of Sines here:
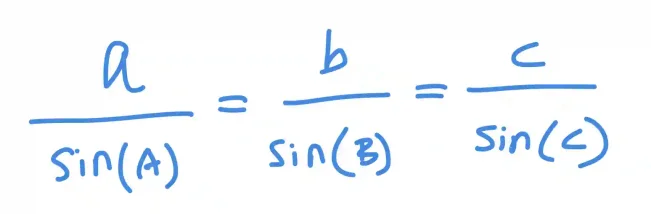
For example, if you know A=40°, B=70°, and side a=10, then the third angle is C=70°. Using the sine law,
Solving gives b=10×sin(70°)sin(40°)≈15.0. This method is ideal for triangles where you have enough angle information to establish clear ratios.
Calculating the missing length given two sides
When you know two sides but not the included angle (the SSA case), you can’t find one unique triangle — there might be one, two, or even no possible triangles. This is sometimes called the ambiguous case of the Law of Sines, since the same sine value can correspond to two different angles.
However, if you just want to know what range of values the missing side could take — without finding exact triangles — geometry gives us a useful constraint known as the triangle inequality.
The triangle inequality theorem states that the length of any side of a triangle must be less than the sum of the other two sides, and greater than their difference.
Mathematically:
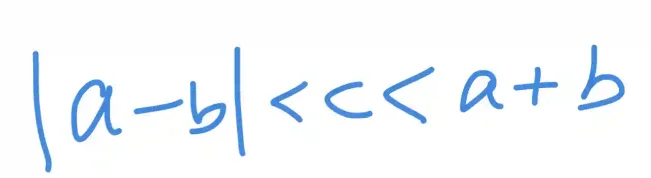
This inequality defines the full range of possible lengths for the third side c.
For example, if the two known sides are 5 and 8, then the third side must satisfy 3<c<13.
That means the missing side could be any length between 3 and 13 (but not including the endpoints). Any value outside this range would make it impossible to form a valid triangle.
Reconciling the Triangle Inequality and the ‘0–1–2 Triangles’ Rule
At first glance, it may seem contradictory that the triangle inequality gives a whole range of possible lengths for the missing side — suggesting infinitely many triangles — while the Law of Sines sometimes tells us there can be zero, one, or two triangles. The difference lies in what each idea describes. The triangle inequality is purely geometric: it tells us the basic conditions that any three side lengths must satisfy to form some triangle. For example, if two sides are 5 and 8, the third side can be any length greater than 3 but less than 13. Within that continuous range, infinitely many triangles could exist in theory.
However, when you bring angles into the picture — for instance, if you know one of the triangle’s angles in addition to two sides — the situation becomes more constrained. The Law of Sines applies in this case, and because the sine function can take the same value for two different angles (like 40° and 140°), you can sometimes get two distinct triangles that satisfy the given data. In other situations, the data might be inconsistent, leading to no possible triangle at all.
So in essence, the triangle inequality defines the range of geometric possibility, while the Law of Sines determines the specific number of valid triangles that fit your exact measurements. Both are correct—they just describe different levels of detail about how a triangle can exist.
Summary
Finding the missing side of a triangle depends entirely on what kind of triangle you have and which pieces of information are given. For right triangles, the Pythagorean theorem is the go-to tool, with special shortcuts available for 30-60-90 and 45-45-90 triangles whose side ratios always stay the same. These relationships let you calculate any missing side using simple multiplication or division.
For non-right triangles, trigonometry takes over. The Law of Cosines is used when two sides and the included angle are known, while the Law of Sines helps when you know one side and two angles. In more complex cases, such as when two sides and a non-included angle are known, you may encounter the ambiguous case, where one, two, or no triangles can satisfy the given data.
Finally, even when exact values aren’t known, the triangle inequality theorem provides an important geometric boundary — the third side of a triangle must always be greater than the difference of the other two sides and less than their sum. Together, these principles form a complete toolkit for calculating any missing side of a triangle, no matter its shape or configuration.
