Kodeclik Blog
Multiples of 37
What is special about the number 37? It is a prime number for instance meaning it is divisible by only 37 and 1.
But the more interesting thing about 37 is that if you multiply it by multiples of 3, i.e., 3,6,9, like in the Python program below:
for i in range(1,10):
print("37 X " + str(i*3) + " = " + str(37 * i * 3))we get this beautiful pattern:
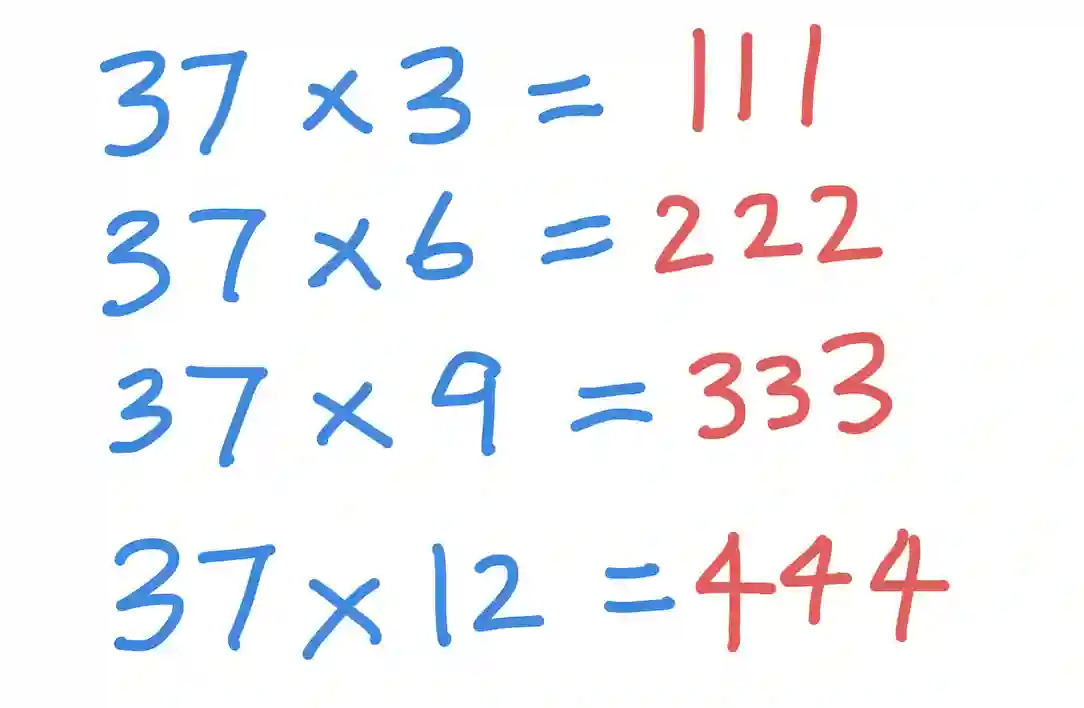
37 X 3 = 111
37 X 6 = 222
37 X 9 = 333
37 X 12 = 444
37 X 15 = 555
37 X 18 = 666
37 X 21 = 777
37 X 24 = 888
37 X 27 = 999Why is this true? Well if you can understand that 37 times 3 is 111, every line after that is just a multiple of 111. 111 is a composite number made up of two primes, viz. 37 and 3.
The pattern starts to “break down” if you continue beyond this (i.e., by changing the index of the for loop):
37 X 30 = 1110
37 X 33 = 1221
37 X 36 = 1332
37 X 39 = 1443
37 X 42 = 1554
37 X 45 = 1665
37 X 48 = 1776
37 X 51 = 1887
37 X 54 = 1998
37 X 57 = 2109Or at the least it is not very nicely apparent. To really continue the original pattern, you can add a “0” and create a number like “37037”. Thus if we update our Python program to:
for i in range(1,10):
print("37037 X " + str(i*3) + " = " + str(37037 * i * 3))we get:
37037 X 3 = 111111
37037 X 6 = 222222
37037 X 9 = 333333
37037 X 12 = 444444
37037 X 15 = 555555
37037 X 18 = 666666
37037 X 21 = 777777
37037 X 24 = 888888
37037 X 27 = 999999Rule for divisibility by 37 = rotating multiples of 37
One rule of divisibility by 37 states that a three-digit number is divisible by 37 if and only if another number, obtained by transferring the first digit to the end of the original number, is also divisible by 37.
For example, the number 148 is divisible by 37 because when the 1 is transferred to the end, it becomes 481, which is also divisible by 37. This rule can be used as a quick test to check the divisibility of a three-digit number by 37.
Let us try it with 370. Modifying this by the above rule gives us 703. Both 370 and 703 are divisible by 37, because 370=37*10 and 703 = 37*19.
Note that this rule only applies to three digit numbers!! Formally, we can say that a three-digit number ABC is divisible by 37 if and only if the number BCA is also divisible by 37.
Also note that you can repeat this rule again. So if XYZ is divisible by 37, we can do one rotation and obtain YZX, another multiple of 37. We can do another rotation on YZX to obtain ZXY, yet another multiple of 37.
Thus, three digit multiples of 37 occur in triples: (XYZ, YZX, ZXY).
Be careful with this rule though! Not all rotations work. Only the first digit moved to the end will work. For instance, from XYZ, if XYZ is a multiple of 37, it doesn’t mean that ZYX is also a multiple of 37. (It had to be ZXY as mentioned above.)
Here is a Python program to print all the three digit multiples of 37 as tuples of digits:
def split_digits(n):
return (n // 100, (n // 10) % 10, n % 10)
for i in range(100,1000):
(h,t,u) = split_digits(i)
if (i % 37 == 0):
print((h,t,u))The above Python program defines a function split_digits to split a three-digit number into its hundreds, tens, and ones digits, and then it iterates through all three-digit numbers (from 100 to 999). For each number, it checks if the number is divisible by 37. If it is, it prints the tuple of its hundreds, tens, and ones digits.
If you run this program you get:
(1, 1, 1)
(1, 4, 8)
(1, 8, 5)
(2, 2, 2)
(2, 5, 9)
(2, 9, 6)
(3, 3, 3)
(3, 7, 0)
(4, 0, 7)
(4, 4, 4)
(4, 8, 1)
(5, 1, 8)
(5, 5, 5)
(5, 9, 2)
(6, 2, 9)
(6, 6, 6)
(7, 0, 3)
(7, 4, 0)
(7, 7, 7)
(8, 1, 4)
(8, 5, 1)
(8, 8, 8)
(9, 2, 5)
(9, 6, 2)
(9, 9, 9)Note that there are approximately 3 numbers (ie 3 multiples of 37) for every 100. But we also know that these numbers can be grouped in terms of rotations, i.e., 148, 481, and 814 are all rotations of each other. Let us update our Python program to print the same numbers as above but grouped by rotations:
def split_digits(n):
return (n // 100, (n // 10) % 10, n % 10)
multipleslist = []
for i in range(100,1000):
(h,t,u) = split_digits(i)
if (h == t == u):
multipleslist.append([(h,t,u)])
elif (i % 37 == 0):
if ((h <= t or t == 0) and (h <= u or u == 0)):
if (t != 0 and u != 0):
multipleslist.append([(h,t,u),(u,h,t),(t,u,h)])
elif (t == 0):
multipleslist.append([(h,t,u),(u,h,t)])
elif (u == 0):
multipleslist.append([(h,t,u),(t,u,h)])
for x in multipleslist:
print(x)The output of this program will be:
[(1, 1, 1)]
[(1, 4, 8), (8, 1, 4), (4, 8, 1)]
[(1, 8, 5), (5, 1, 8), (8, 5, 1)]
[(2, 2, 2)]
[(2, 5, 9), (9, 2, 5), (5, 9, 2)]
[(2, 9, 6), (6, 2, 9), (9, 6, 2)]
[(3, 3, 3)]
[(3, 7, 0), (7, 0, 3)]
[(4, 0, 7), (7, 4, 0)]
[(4, 4, 4)]
[(5, 5, 5)]
[(6, 6, 6)]
[(7, 7, 7)]
[(8, 8, 8)]
[(9, 9, 9)]See how neatly this program groups the multiples into equivalence classes by rotation?
How does the above program work? It looks a little bit complicated but easy to explain in pieces. As before we are searching all three digit numbers and then checking for divisibility by 37. We keep a running list of numbers and groups discovered in the variable called “multipleslist”. For numbers that are triples of the same digit, like 111, 222, we simply append that triple to our running list and move on. If they are not triples, we first verify that they are indeed a multiple of 37, and once we confirm they are, we subject them to more tests. We first see if the same (h,t, u) triple, i.e. returned by split_digits, could have been encountered earlier. This would have happened if t was less than h, or if u was less than h (and only for the opposite of these conditions we proceed further). We “excuse” the cases where either u or t is zero (in which case this is likely the first time we are encountering them because remember that we are searching for three digit numbers). Inside the main loop, we add not just the current multiple of 37 discovered but also its rotations (according to the above rule). Again we take care not to add multiples where the hundreds digit is 0 (because we are only interested in three digit multiples).
After (4,4,4) notice that the rotations are not present anymore (because they have already been discovered earlier as a variant of a previous multiple).
Proof of rotating multiples of 37
But why does the rotating multiple idea work? Here is a very simple proof. There are other nice resources about this such as John Cook’s blog and the proof below is along the same lines as shown there.
Let's consider a three-digit number with digits xyz, such that the number n = 100x+10y+z is divisible by 37. This means that n = 37k for some value of k. In the rotating multiple idea, we construct a new number with digits zxy (so that the number becomes 100z + 10x + y) and we need to prove that zyx is also divisible by 37.
To prove this, we can use the fact that 999 = 37*27 (ie a multiple of 37) and so we can add 999z to n to get another multiple of 37:
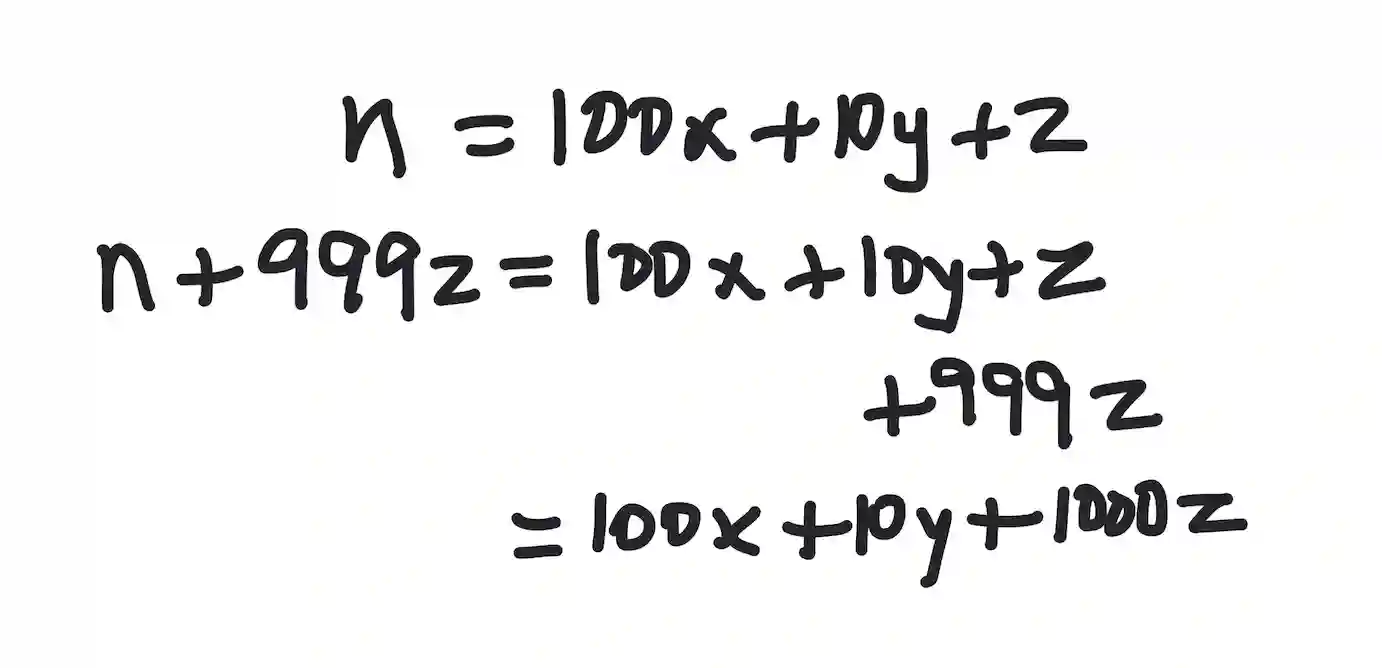
Now this new number is clearly divisible by 10, and since 10 and 37 are relatively prime (they have no common factors other than 1), we can divide the entire expression by 10 and maintain divisibility by 37:
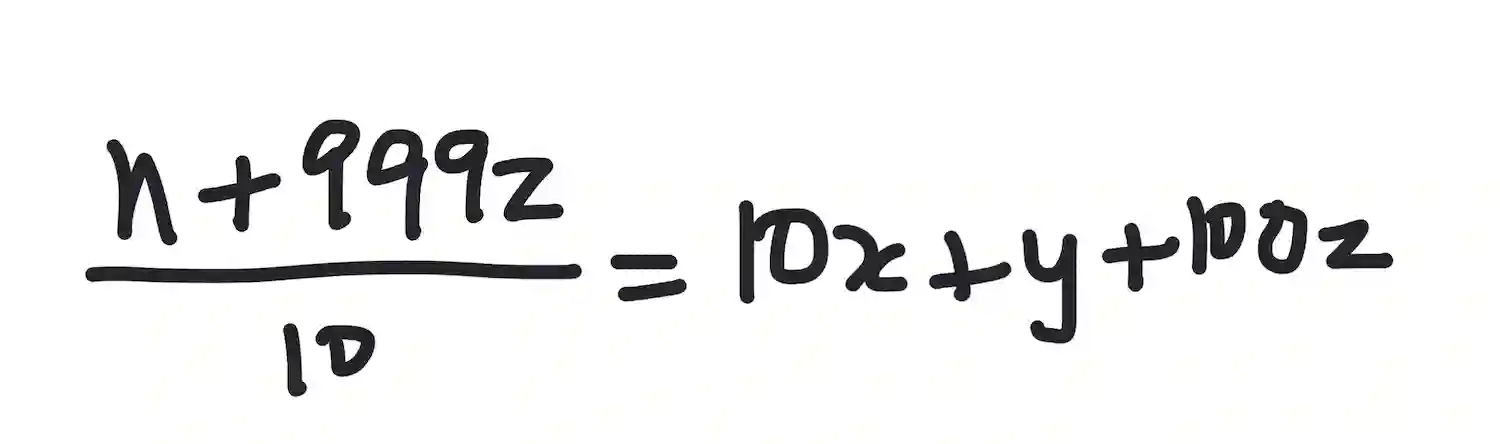
But this expression is indeed the rotated number we were looking for, ie with digits zxy. Since we obtained zxy by dividing a multiple of 37 by 10, it must also be a multiple of 37. Therefore this number is also divisible by 37!
In summary, the proof relies on the fact that adding a multiple of 999 to a number does not change its divisibility by 37, and since 999 is 27 times 37, we can rotate the digits of a three-digit number divisible by 37 to get another number that is also divisible by 37.
Note that we can continue rotating it again (as shown in the Python program above) to obtain more multiples of 37.
Note as stated before that this “rotating multiple” theorem applies specifically to three-digit numbers and the number 37. It does not necessarily hold true for other numbers or for numbers with more or fewer digits.
Another 37 Mirroring Trick
We will leave you with a final, mysterious, 37 trick. Are you ready for this?
Any multiple of 37 can be mirrored and spaced with a zero each for another multiple of 37.
For example, 37 is a multiple of 37. We mirror it, to get 73, then add a zero, to get 703 and voila, 703 is a multiple of 37!
Similarly, from 74 we can get 407 as another multiple of 37.
From 518, we get 80105 (notice how we add zeros between every successive pair in the reversed 815), and 80105 is a multiple of 37.
Finally, 32856 is a multiple of 37 (32856 is 37 times 888). We reverse it to get: 65823 and we pad zeros to get: 605080203 which is a multiple of 37 as well (16353519 times 37).
If you liked exploring Math with Python, checkout our blogpost on Fibonacci numbers!
Want to learn Math or Python with us? Sign up for 1:1 or small group classes.