Kodeclik Blog
Accessing the Boltzmann Constant in Python
The Boltzmann constant is a physical constant used in physics and chemistry to describe the relationship between temperature, energy, and the thermodynamics of gases. More specifically, it connects the relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. This fundamental physical constant plays a crucial role in various areas of physics and chemistry, bridging the gap between microscopic and macroscopic phenomena.
What is the value of the Botzmann constant?
The Boltzmann constant (k) is a physical constant equal to 1.3806 x 10^-23 joules/kelvin (J/K). It was first proposed by Ludwig Boltzmann in 1877 as part of his statistical mechanics theory of thermodynamics. This means that for every Kelvin increase in temperature, there will be an increase in energy by 1.38 x 10^-23 Joules (or 0.0000000000138 Joules). (Note that temperature must be in Kelvin, not Fahrenheit or Celsius). That might not sound like a lot, but if you consider this on a large scale, it adds up quickly! The Boltzmann constant is one of the seven key constants in physics that you should know about.
The famous equation involving the Boltzmann constant PV = NkT states that the product of pressure (P) and volume (V) equals the product of N (the number of molecules of gas), T (absolute temperature), and k, the Boltzmann constant. This equation highlights that there exists a direct connection between several key physical variables through the Boltzmann constant.
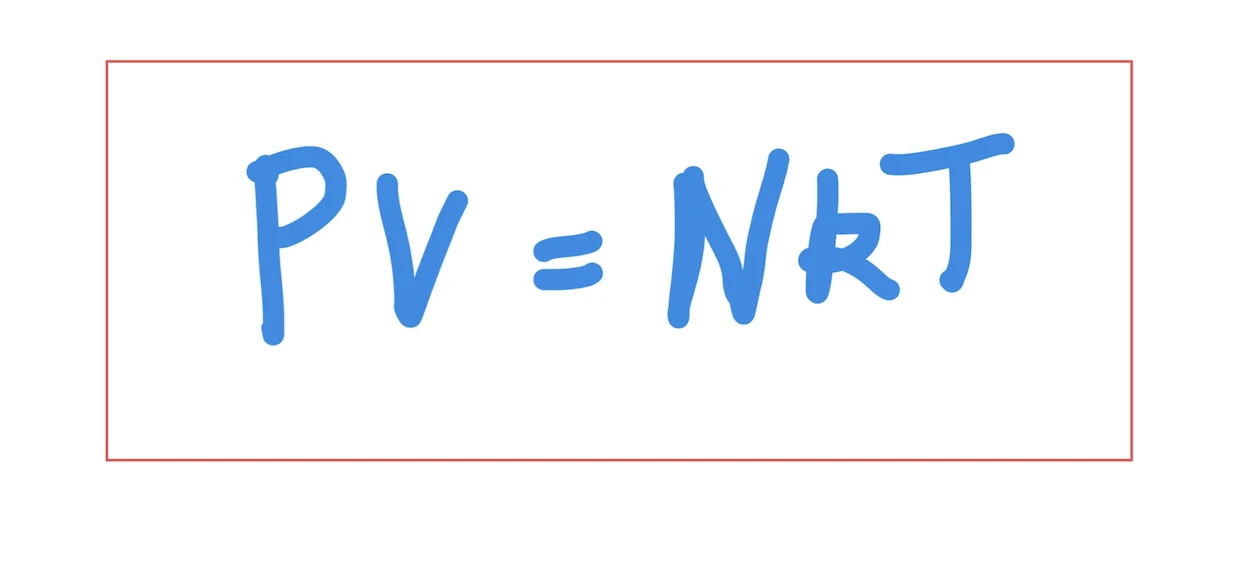
Applications of the Boltzmann Constant
The reason the Boltzmann constant is so important is that it captures phenomena at both macroscopic and microscopic levels. At a macroscopic level, it explains why certain systems have different levels of energy; for example, why hot water has more energy than cold water or why air heats up when compressed.
At a microscopic level, it explains why certain molecules are more likely to react with each other than others; for example, why some molecules are more likely to form bonds than others or why some molecular interactions require more energy than others. It also helps us understand how chemical reactions work on an atomic level by providing insight into how molecules interact with each other due to differences in their energies.
One of the most important applications of the Boltzmann constant is in the study of black body radiation. It appears in the Stefan-Boltzmann constant, which describes the total energy radiated by a black body as a function of its temperature. The Stefan-Boltzmann constant is directly related to the Boltzmann constant, emphasizing the latter's significance in understanding thermal radiation and energy transfer processes.
The Boltzmann constant is also closely related to other fundamental constants. For instance, it can be expressed as the ratio of the gas constant to the Avogadro constant. This relationship highlights the connection between the behavior of individual particles and the properties of macroscopic systems. The gas constant, which appears in the ideal gas law, can be thought of as the Boltzmann constant multiplied by Avogadro's number, providing a link between molecular-scale and bulk properties of gases.
Accessing the Boltzmann Constant in Python
To access the Boltzmann constant in Python, we use scipy.constants, a library of mathematical constants that provides access to hundreds of physical constants.
To get started, we will first need to install scipy.constants. You can do so by running pip install scipy on your terminal or command prompt if you are using Windows. Once installed, we can easily import this library into our project like so:
import scipy.constants as sc
print(sc.k)
print(sc.Boltzmann)Here we have imported the package as “sc” and henceforth all constants can be accessed as part of “sc”. The Boltzmann constant can be accessed as either sc.Boltzmann or sc.k (see equation above). Thus both these statements produce the same result. The output of the program will be:
1.380649e-23
1.380649e-23as expected. Note that the above values are in J K^-1 units.
Accessing the Boltzmann Constant in other Units
It turns out scipy.constants supports the access of the Boltzmann constant in other units as well. For this, it provides a dictionary of physical constants, of the format physical_constants[name] = (value, unit, uncertainty). We can access the Boltzmann constant in J K^-1 units as well as in other units by providing a suitable name. For instance:
print (sc.physical_constants['Boltzmann constant'])outputs:
(1.380649e-23, 'J K^-1', 0.0)In other words, the output says that 1.380649e-23 is the value with units J K^-1 and uncertainty 0.0. We can try other names for the Boltzmann constant, like so:
import scipy.constants as sc
print (sc.physical_constants['Boltzmann constant'])
print (sc.physical_constants['Boltzmann constant in eV/K'])
print (sc.physical_constants['Boltzmann constant in Hz/K'])
print (sc.physical_constants['Boltzmann constant in inverse meter per kelvin'])The output will be:
(1.380649e-23, 'J K^-1', 0.0)
(8.617333262e-05, 'eV K^-1', 0.0)
(20836619120.0, 'Hz K^-1', 0.0)
(69.50348004, 'm^-1 K^-1', 0.0)thus providing you a rich vocabulary of units to choose from.
Example: Finding the speed of oxygen molecules in air
Here is a Python program to calculate the root mean square speed of oxygen molecules in air at room temperature (20°C or 293.15 K).
To solve this, we can use the formula for root mean square speed: v = sqrt(3kT/m) where k is the Boltzmann constant, T is the temperature in Kelvin, and m is the mass of an oxygen molecule.
import numpy as np
from scipy import constants
# Temperature in Kelvin
T = 293.15 # 20°C
# Mass of an oxygen molecule in kg
m_oxygen = 32 * constants.atomic_mass # Oxygen has an atomic mass of 16, and O2 has 2 atoms
# Calculate root mean square speed
v_rms = np.sqrt(3 * constants.k * T / m_oxygen)
print(f"The root mean square speed of oxygen molecules at 20°C is: {v_rms:.2f} m/s")The above code begins by importing the necessary libraries: numpy for mathematical operations and scipy.constants for accessing physical constants. The code then sets the temperature in Kelvin and calculates the mass of an oxygen molecule using the atomic mass constant from scipy.constants, considering that an oxygen molecule (O2) consists of two oxygen atoms.
As you can see, the core of the calculation lies in the formula for root mean square speed, which is implemented using numpy's square root function and scipy's Boltzmann constant. This formula relates the temperature and mass of the molecules to their average speed, showcasing how the Boltzmann constant bridges macroscopic properties (temperature) with microscopic behavior (molecular speed). Finally, the code prints the result, formatting it to two decimal places and including the appropriate units.
This code will output:
The root mean square speed of oxygen molecules at 20°C is: 461.17 m/sThis example demonstrates a practical application of statistical mechanics and thermodynamics in understanding molecular motion in gases.
Summary
In summary, accessing the Boltzmann constant in Python is easy and straightforward once you have installed SciPy Constants! With just one line of code, you can easily retrieve the value of this constant in a range of units! As a programmer, having quick access to this important physical constant can help save time when coding programs related to physics or thermodynamics! Whether it’s for school projects or research work, knowing how to quickly retrieve this data makes programming much easier and more efficient!
If you are compare our discussion here with what you might see in your science textbook, you might note that different books list the constant's value in different unit systems, emphasizing its universal nature. The precise value of 1.380649 × 10-23 J K-1 is a result of the 2019 redefinition of SI base units, which fixed the Boltzmann constant to this exact value, further cementing its fundamental role in modern physics and metrology.
If you liked this blogpost, learn how to access Euler’s number in Python!
Want to learn Python with us? Sign up for 1:1 or small group classes.
