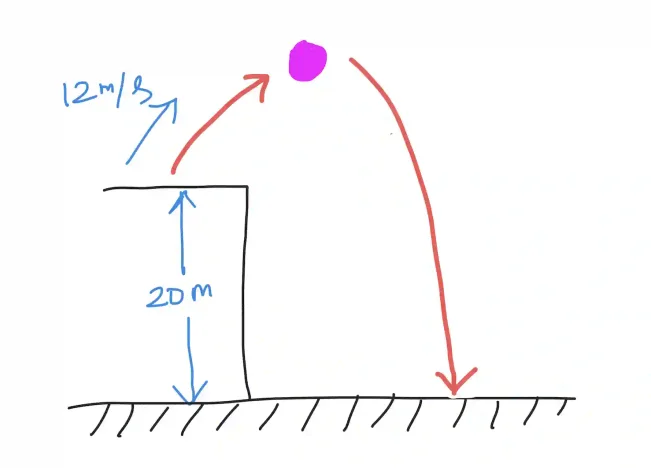
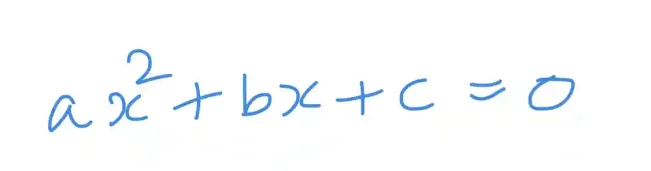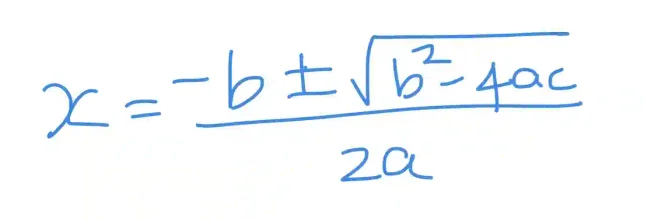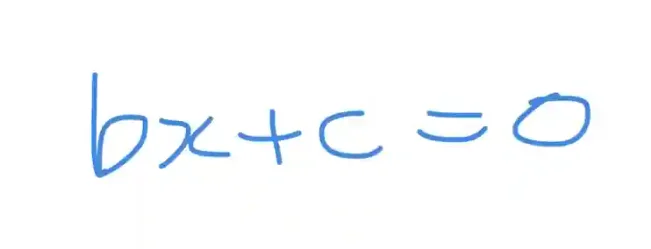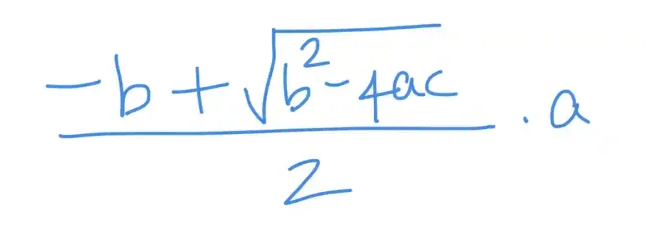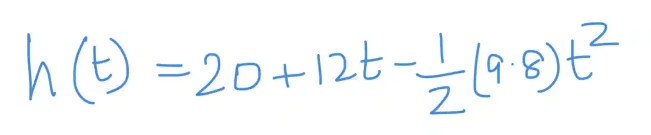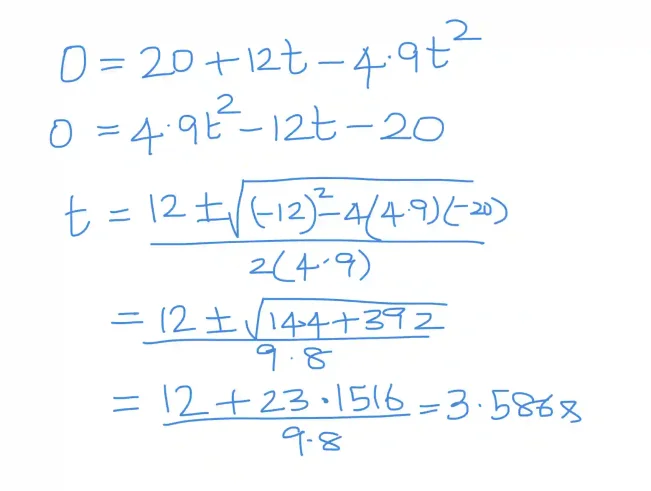About
Kodeclik is an online coding academy for kids and teens to learn real world programming. Kids are introduced to coding in a fun and exciting way and are challeged to higher levels with engaging, high quality content.
Popular Classes
Scratch Coding
Minecraft Coding
TinkerCAD
Roblox Studio
Python for Kids
Javascript for Kids
Pre-Algebra
Geometry for Kids
Copyright @ Kodeclik 2025. All rights reserved.