Kodeclik Blog
How to subtract in Hexadecimal
Recall that Hexadecimal is a base-16 number system that uses sixteen distinct symbols: the numbers 0-9 and the letters A-F (or a-f), where A represents 10, B represents 11, C represents 12, D represents 13, E represents 14, and F represents 15.
This number system is extensively used in computing and digital systems because it provides a more concise way to represent binary numbers, as each hexadecimal digit perfectly represents four binary digits (bits). For example, the hexadecimal number A5 is equal to 165 in decimal (10 × 16¹ + 5 × 16⁰ = 160 + 5 = 165) and 10100101 in binary. It is 10100101 because the first four digits (1010) denote 10 (in decimal), i.e., A (in hexadecimal) and the second four digits (0101) denote 5 (in decimal as well as hexadecimal).
Hexadecimal notation is commonly used in programming for tasks such as representing memory addresses, defining colors in web development (where colors are specified using six hexadecimal digits, like #FF0000 for pure red), and debugging computer programs. The prefix "0x" is often used to denote hexadecimal numbers in programming languages (e.g., 0xFF), while the suffix "h" is sometimes used in other contexts (e.g., FFh).
In this blogpost we will learn how to do hexadecimal subtraction, i.e., how to subtract one hexadecimal number from another.
Hexadecimal subtraction is performed just like regular subtraction (in decimal) except when borrowing in hex, the "1" that is borrowed represents 16 (decimal) rather than 10 (decimal). Let us learn through a few examples!
Example 1: Simple Subtraction
When subtracting 7 from B, i.e. computing B-7, we first convert B to its decimal value, i.e., 11. The subtraction then becomes straightforward: 11 - 7 = 4. This example shows how simple hexadecimal subtraction can be when no borrowing is required.
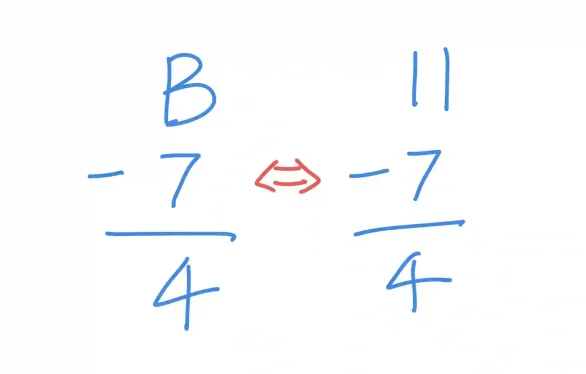
Example 2: Subtraction with Borrowing
Let's solve 26A - 6F.

Starting with the rightmost column, we cannot subtract F (15) from A (10), so we must borrow 16 from the next column. The 6 becomes 5, and A becomes 26 (16 + 10). Now we can subtract 15 from 26, giving us 11 (B). Moving to the middle column, we cannot subtract 6 from 5, so we borrow again. The 2 becomes 1, and 5 becomes 21. Subtracting 6 from 21 gives us 15 (F). Finally, in the leftmost column, we have 1 - 0 = 1. The complete answer is 1FB.
Example 3: Subtraction with Larger Numbers
Let us try doing A57-125.
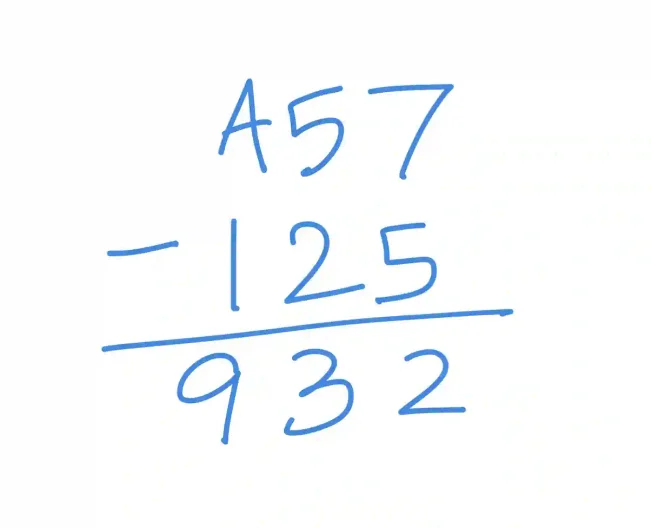
For A57 - 125, we can work from right to left without borrowing. In the rightmost column, 7 - 5 = 2. In the middle column, 5 - 2 = 3. In the leftmost column, A (10) - 1 = 9. This gives us our final answer of 932. This example demonstrates how straightforward hexadecimal subtraction can be when no borrowing is required.
Example 4: Complex Borrowing Subtraction
Finally, let us do a complex borrowing with multiple digits, BC5 - 1DA.
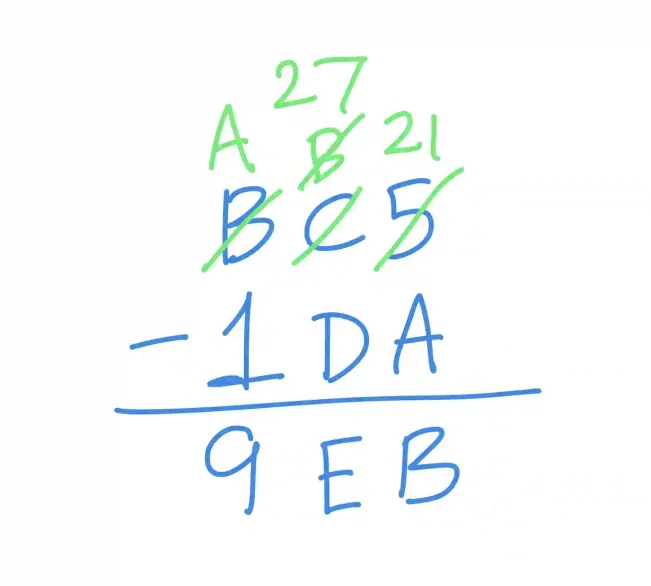
Starting with the rightmost column, we need to subtract A (10) from 5. Since this isn't possible directly, we borrow 16, making 5 become 21. Now we can subtract 10 from 21, giving us 11 (B). Moving to the middle column, we need to subtract D (13) from B (11). We borrow again, making B become 27, allowing us to subtract 13 and get 14 (E). Finally, in the leftmost column, we have B - 1 = 9. Our final answer is 9EB.
The key to successful hexadecimal subtraction in all of the above, is remembering that when borrowing, we add 16 (not 10) to the digit, and that A through F represent the values 10 through 15 respectively. Working from right to left, just as in decimal subtraction, helps maintain a systematic approach to solving these problems.
Hexadecimal Subtraction Table
If you would like to go old school, below is a handy hexadecimal subtraction table that you can use. We actually generated this subtraction table using Python!
def generate_hex_subtraction_table():
# Generate hex digits 0-F
hex_digits = [f'{i:X}' for i in range(16)]
# Create and print the header row
print("\nHexadecimal Subtraction Table")
print(" |", end=" ")
for digit in hex_digits:
print(f" {digit}", end=" ")
print("\n--+" + "-" * 48)
# Generate and print each row of the table
for minuend in hex_digits:
print(f"{minuend} |", end=" ")
for subtrahend in hex_digits:
diff = (int(minuend, 16) - int(subtrahend, 16)) % 16
print(f" {diff:X}", end=" ")
print()
# Generate and display the table
generate_hex_subtraction_table()The program defines a function generate_hex_subtraction_table() that first generates a list of hexadecimal digits from 0 to F. The main part of the program iterates through each possible minuend (the number being subtracted from) and subtrahend (the number being subtracted), calculating their difference using base-16 arithmetic. Each result is formatted in hexadecimal notation and displayed in a grid format, where the leftmost column represents the minuend and the top row shows the subtrahend.
| 0 1 2 3 4 5 6 7 8 9 A B C D E F
--+------------------------------------------------
0 | 0 F E D C B A 9 8 7 6 5 4 3 2 1
1 | 1 0 F E D C B A 9 8 7 6 5 4 3 2
2 | 2 1 0 F E D C B A 9 8 7 6 5 4 3
3 | 3 2 1 0 F E D C B A 9 8 7 6 5 4
4 | 4 3 2 1 0 F E D C B A 9 8 7 6 5
5 | 5 4 3 2 1 0 F E D C B A 9 8 7 6
6 | 6 5 4 3 2 1 0 F E D C B A 9 8 7
7 | 7 6 5 4 3 2 1 0 F E D C B A 9 8
8 | 8 7 6 5 4 3 2 1 0 F E D C B A 9
9 | 9 8 7 6 5 4 3 2 1 0 F E D C B A
A | A 9 8 7 6 5 4 3 2 1 0 F E D C B
B | B A 9 8 7 6 5 4 3 2 1 0 F E D C
C | C B A 9 8 7 6 5 4 3 2 1 0 F E D
D | D C B A 9 8 7 6 5 4 3 2 1 0 F E
E | E D C B A 9 8 7 6 5 4 3 2 1 0 F
F | F E D C B A 9 8 7 6 5 4 3 2 1 0 How do you use this table? For example, to subtract 7 from A, find row A and column 7, and the intersection shows the result 3. Thus A-7=3. Thus, the intersection of any row and column displays their hexadecimal difference, with negative results handled using modulo 16 arithmetic.
This table serves as a valuable reference tool for various applications including in programming or simply to test your work!
When to subtract in hexadecimal: color adjustment
A good practical example of hexadecimal subtraction is in color manipulation. For instance, if you would like to darken a color, we can subtract a certain fixed amount from it to create darker shades.
Consider pure red (#FF0000). If you subtract #220000, you are left with #DD0000 which is a darker shade of red.

If you liked this blogpost and would like to learn more about number systems such as covered in the ACSL competition, or if you would like to learn Python, checkout our online coding classes.