Quadrants in Math

We will learn about quadrants in math, specifically quadrants in two dimensional cartesian geometry.

As the name suggests, a quadrant means “one fourth” and refers to a quarter of the cartesian plane defined by the x- and y-axes.

In the cartesian plane, the x-axis and y-axis are at right angles to each other and the point at which they intersect is called the origin.

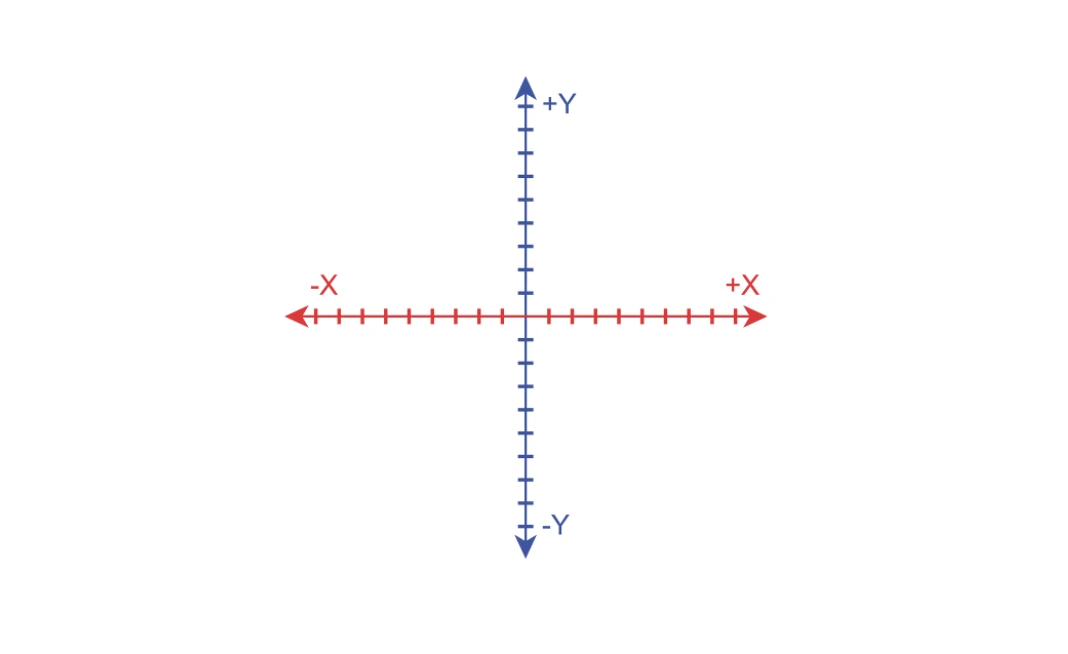
The four quadrants

As the picture above shows the quadrants are named Quadrants I, II, III, and IV starting from the (top, right) quadrant and moving in the counter-clockwise direction. Points in Quadrant I (top right) have x-values positive and y-values positive. Points in Quadrant II (top, left) have x-values negative and y-values positive. Points in Quadrant III (bottom, left) have both x- and y-values to be negative. Finally, points in Quadrant IV (bottom, right) have x-values positive but y-values negative. The above figure gives you a handy way to remember the signs of quadrants.

Locating points

The origin of the cartesian plane is denoted by (0,0). All points are specified relative to the origin and have two values. These two values are referred to as the x-coordinate and the y-coordinate, respectively. Thus, the origin has x-coordinate zero and the y-coordinate as zero as well. The x-coordinate is alternatively referred to as the abscissa and the y-coordinate is referred to as simply the ordinate.

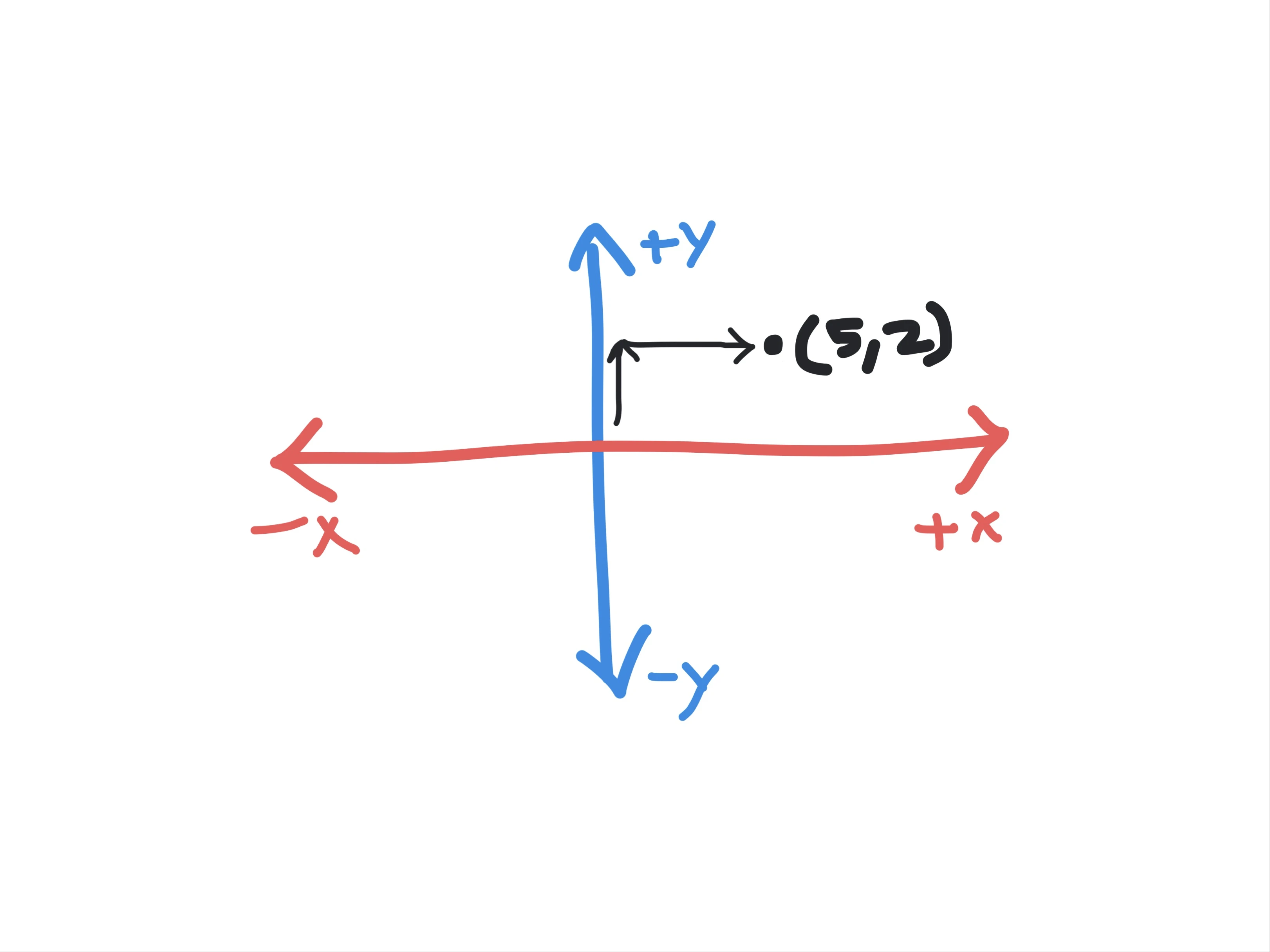
Let us try to locate the point (5,2) on the cartesian plane. We need to move 5 steps to the right (because it is a positive integer) and move 2 steps up (because again it is positive) to find the point, as shown below:

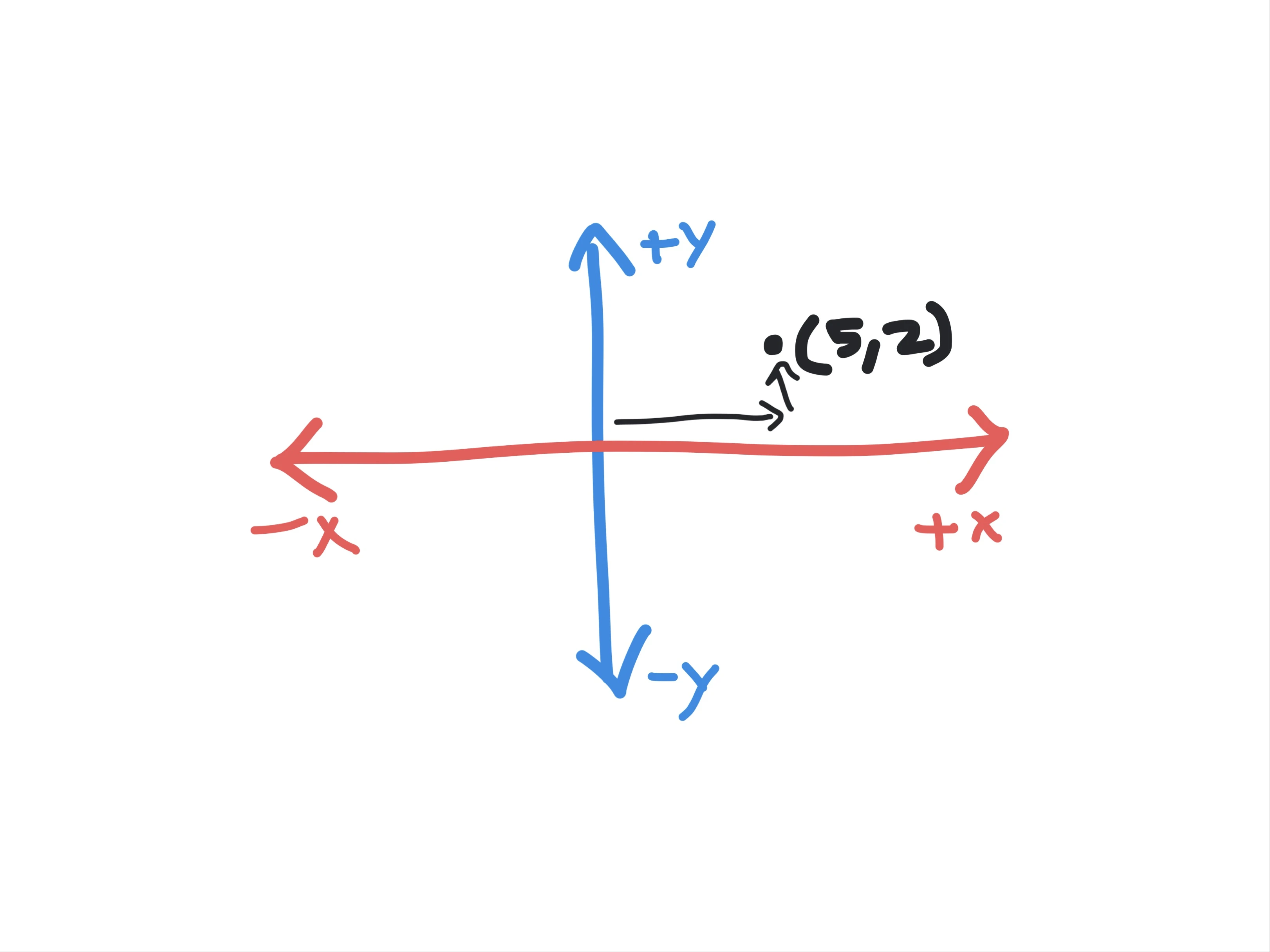
Thus, the x-coordinate or the abscissa specifies the horizontal distance of your point from the origin and by looking at the sign we can glean whether we need to move right or left from the origin. Similarly, the y-coordinate or the ordinate specifies the vertical distance of the point from the origin and the sign indicates whether we should move up or down from the origin.

Note that because the x-axis and y-axis are orthogonal to each other (i.e., they are in two different directions, at 90 degrees to each other) you could move 5 steps to the right and then 2 steps up, or vice versa, i.e., 2 steps up and then 5 steps to the right.

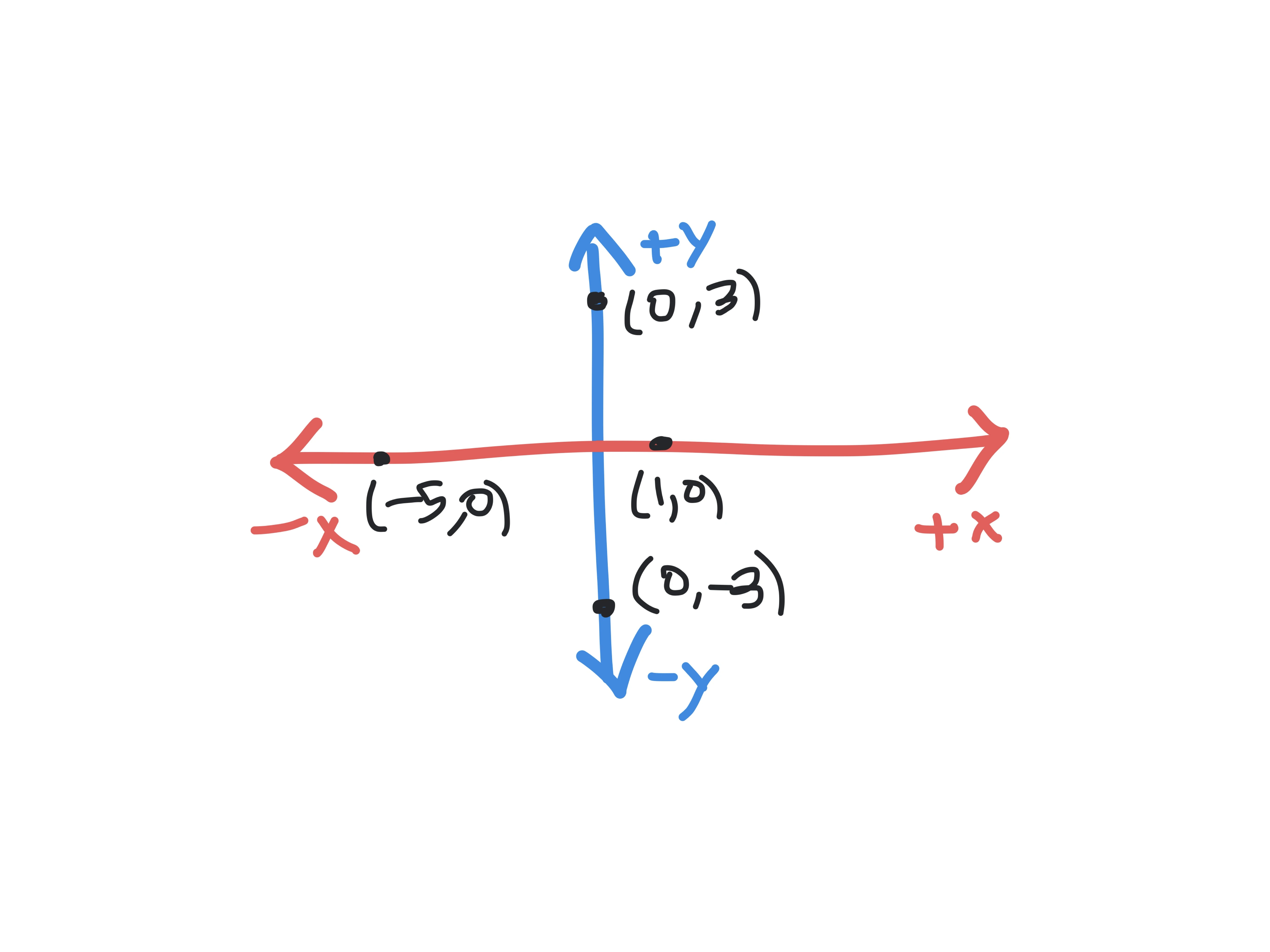
Because of the way the cartesian plane is designed, points that have a y-coordinate of 0 lie on the x-axis. Similarly, points that have a x-coordinate of 0 lie on the y-axis, as shown below:

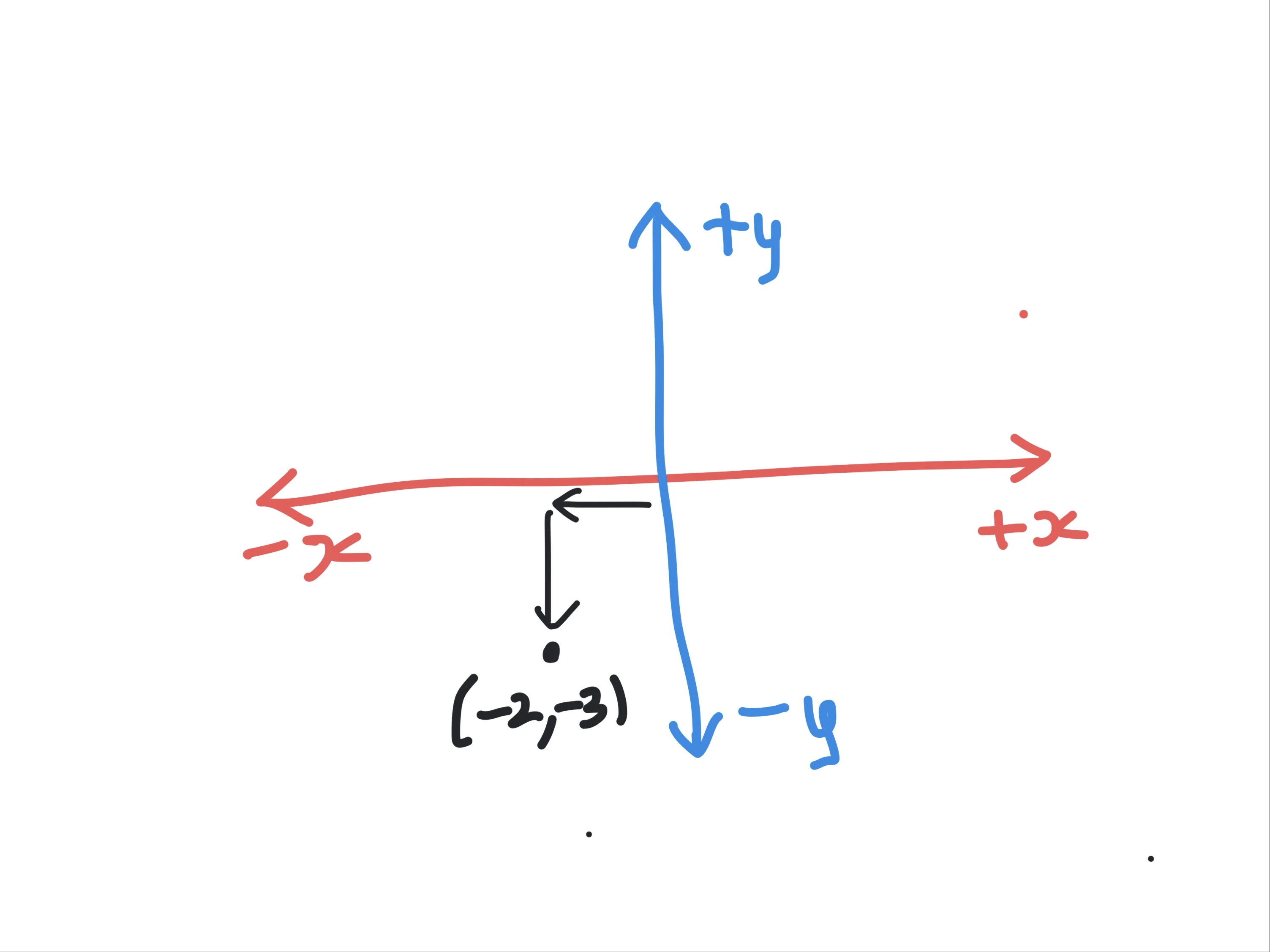
As a final example, let us take a point (-2,-3) where both coordinates are negative. From this we can conclude that we must move left from the origin and down from the origin to locate the given point. Hence the point must be in Quadrant III as shown below.

If you liked this blogpost, checkout our article on sequences.