Kodeclik Blog
How to convert a vector into a square matrix
We will learn a simple approach here to convert a (column) vector into a square matrix. But first, what is a vector?
A vector is simply a one-dimensional array of numbers arranged vertically. In mathematical notation, it's typically represented as a single row or column of numbers enclosed in square brackets or parentheses. In linear algebra and many computational applications, vectors are fundamental structures for representing data and performing calculations.
For instance, consider the following examples of vectors:
Weather Data
We could use a vector to represent daily temperatures for a week, useful in meteorology or climate studies. Consider the following code:
import numpy as np
# Daily temperatures (°C) for a week
temperatures = np.array([22, 24, 23, 25, 21, 20, 22])
print("Weekly temperatures:\n", temperatures)The output will be:
Weekly temperatures:
[22 24 23 25 21 20 22]Note that the output is printed as a row vector, i.e., one row having lots of columns.
We could also view the array in terms of a column vector, i.e., having one column with lots of rows. The way to do that will be:
import numpy as np
# Daily temperatures (°C) for a week
temperatures = np.array([22, 24, 23, 25, 21, 20, 22]).reshape(-1, 1)
print("Weekly temperatures:\n", temperatures)The output here will be:
Weekly temperatures:
[[22]
[24]
[23]
[25]
[21]
[20]
[22]]Note that we now have multiple rows, but each row is really only a single column. The reshape(-1, 1) operation in this code is used to explicitly format the given array into a column vector.
The (-1,1) as arguments to reshape might appear strange. But it will make sense once you understand what these arguments are supposed to convey. The -1 in the first position tells NumPy to automatically calculate the number of rows needed based on the total number of elements and the specified number of columns. The 1 in the second position specifies that we want only one column. Thus, we are essentially converting the given array into a column vector.
Financial Data
You could use a vector to represent the closing prices of a stock over the last 5 trading days, used in financial analysis.
import numpy as np
# Stock prices ($) for the last 5 trading days
stock_prices = np.array([145.23, 146.78, 144.56, 147.89, 148.32]).reshape(-1, 1)
print("Stock prices:\n", stock_prices)Population Data
You can use a vector to represent the populations of different cities, useful in urban planning or demographic studies.
import numpy as np
# Population (in millions) of 5 cities
city_populations = np.array([8.4, 3.9, 2.7, 1.5, 0.9]).reshape(-1, 1)
print("City populations (millions):\n", city_populations)Sports Statistics
Finally, you can store a basketball player's scoring performance over several games in a vector and use it for sports analytics.
import numpy as np
# Points scored by a basketball player in the last 6 games
player_scores = np.array([28, 32, 25, 30, 35, 29]).reshape(-1, 1)
print("Player scores:\n", player_scores)All the above examples demonstrate how column vectors can represent various types of real-world data. In each of the above examples, we use the reshape(-1, 1) function to ensure these arrays are treated as column vectors, which is important for many mathematical operations and machine learning algorithms.
Creating a square matrix from a column vector
What does it mean to create a square matrix from a column vector? Note that a column vector, of say size 5, means that it is of dimension 5x1. A row vector of the same size would be 1x5. Thus one way to create a square matrix from a column vector is to multiply these two vectors. Multiplying a 5x1 vector with a 1x5 vector will yield a 5x5 matrix. This is often called the “outer product”.
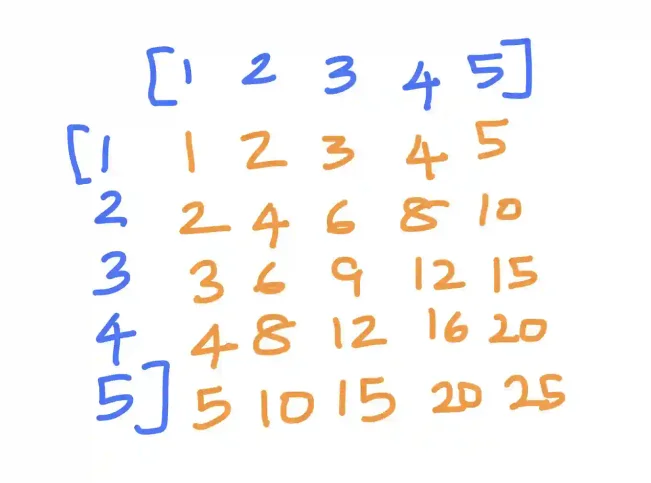
Contrast the outer product with the inner product. In the inner product, you multiply them in the opposite order, i.e., 1x5 times 5x1 will yield a 1x1, i.e., a scalar quantity, a single number.
Method 1: Use np.outer()
Here is a simple example of outer products using numpy:
import numpy as np
# Create a column vector
column_vector = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
# Create a square matrix using outer product
square_matrix = np.outer(column_vector, column_vector.T)
print("Column vector:")
print(column_vector)
print("\nSquare matrix:")
print(square_matrix)In this code, we first create a column vector using NumPy's array function and reshape it to ensure it's a 5x1 vector. Then, we use np.outer() to compute the outer product of the column vector with its transpose (row vector). This operation results in a 5x5 square matrix where each element (i, j) is the product of the i-th element of the column vector and the j-th element of the row vector.
The output will be:
Column vector:
[[1]
[2]
[3]
[4]
[5]]
Square matrix:
[[ 1 2 3 4 5]
[ 2 4 6 8 10]
[ 3 6 9 12 15]
[ 4 8 12 16 20]
[ 5 10 15 20 25]]Now, let's contrast this with the inner product:
import numpy as np
# Create a column vector
column_vector = np.array([1, 2, 3, 4, 5]).reshape(-1, 1)
# Compute inner product
inner_product = np.dot(column_vector.T, column_vector)
print("Inner product:")
print(inner_product)The output here will be:
Inner product:
[[55]]Note the key difference between this code and previous code, i.e., the use of np.outer() versus np.dot() functions. In np.outer(), we list the given column vector followed by its transpose. In np.dot(), we list the transpose first followed by the vector. In fact, if we flipped the order, we can still use np.dot() for computing the outer product.
Method 2: Use np.dot() to compute the outer product
Consider the below code that showcases two ways of computing the outer product:
import numpy as np
# Create a column vector
column_vector = np.array([1, 2, 3, 4]).reshape(-1, 1)
# Create a square matrix from the column vector using np.dot()
square_matrix_dot = np.dot(column_vector, column_vector.T)
# Create a square matrix from the column vector using np.outer()
square_matrix_outer = np.outer(column_vector, column_vector.T)
print(square_matrix_dot)
print(square_matrix_outer)Both these methods will yield the same answer:
[[ 1 2 3 4]
[ 2 4 6 8]
[ 3 6 9 12]
[ 4 8 12 16]]
[[ 1 2 3 4]
[ 2 4 6 8]
[ 3 6 9 12]
[ 4 8 12 16]]Note that we have flipped the order in which we supply arguments to np.dot().
Outer products in general
Note that because both np.dot() and np.outer() take two arguments, there is no requirement that the two arguments be transposes of each other (we have been using transposes for illustration purposes), They could be any two vectors (as long as the dimensions match). Given two vectors of appropriate dimensions, the outer product is simply the matrix formed by multiplying each element of a first vector with every element of the second vector.
For instance, consider the below code:
import numpy as np
# Create two different vectors
a = np.array([1, 2, 3])
b = np.array([4, 5, 6, 7])
# Compute the outer product
result = np.outer(a, b)
print("Vector a:", a)
print("Vector b:", b)
print("Outer product:")
print(result)The output will be:
Vector a: [1 2 3]
Vector b: [4 5 6 7]
Outer product:
[[ 4 5 6 7]
[ 8 10 12 14]
[12 15 18 21]]In other words we began with two vectors of size 3x1 and 4x1 and for each element of the first, we multiplied it with every element of the second. Thus our final outer product is of size 3x4.
Should I use np.dot() or np.outer() to compute outer products?
While both can be used (as we have seen above) to compute outer products, there are important distinctions to be made.
np.outer() is specifically designed for computing outer products. It takes two 1D arrays and computes their outer product, resulting in a 2D array. np.outer() is more explicit about your intention as it is specifically designed for outer products and is thus generally preferred when that's what you're trying to compute.
np.dot() on the other hand is more versatile and can be used for computing many products (including outer products). To use np.dot() for outer products, you need to reshape your vectors properly.
In summary, while both can achieve the same result for outer products, np.outer() automatically unravels its inputs to 1D, while np.dot() requires you to manage the dimensions yourself. For simple outer products, np.outer() might be slightly more optimized, though for most practical purposes, the difference is negligible.
Applications of outer products
In quantum mechanics, outer products are used to construct projection operators and density matrices. A projection operator projects a quantum state onto a specific subspace, which is crucial for measurements and state preparations. For example, if |ψ⟩ represents a quantum state, the outer product |ψ⟩⟨ψ| forms a projection operator onto that state. Density matrices, which describe mixed quantum states, are also constructed using weighted sums of outer products of pure states. These tools are fundamental in quantum information theory and quantum computing.
Signal processing and image compression often utilize outer products. In image compression techniques like singular value decomposition (SVD), an image matrix is decomposed into a sum of outer products of vectors. Each outer product represents a rank-one approximation of the original image, and by selecting the most significant components, the image can be compressed while retaining its essential features. This application of outer products allows for efficient data compression and noise reduction in various types of signals and images.
In machine learning and neural networks, outer products play a role in weight updates during training. For instance, in the backpropagation algorithm used to train neural networks, the weight updates for a layer are often computed as the outer product of the error gradient and the layer's input. This operation efficiently calculates how each weight should be adjusted to minimize the network's error. Outer products are also used in some forms of attention mechanisms in neural networks, allowing the model to focus on relevant parts of the input data.
If you liked this blogpost, checkout our blogposts on numpy.ones and how to convert a python list into a numpy array!
Want to learn Python with us? Sign up for 1:1 or small group classes.