Kodeclik Blog
How are 2D quadrants labeled?
In a 2D coordinate system, the quadrants are labeled in a specific order. They are labeled using Roman numerals, starting from the upper right and going counter-clockwise.
The four quadrants are labeled as follows:
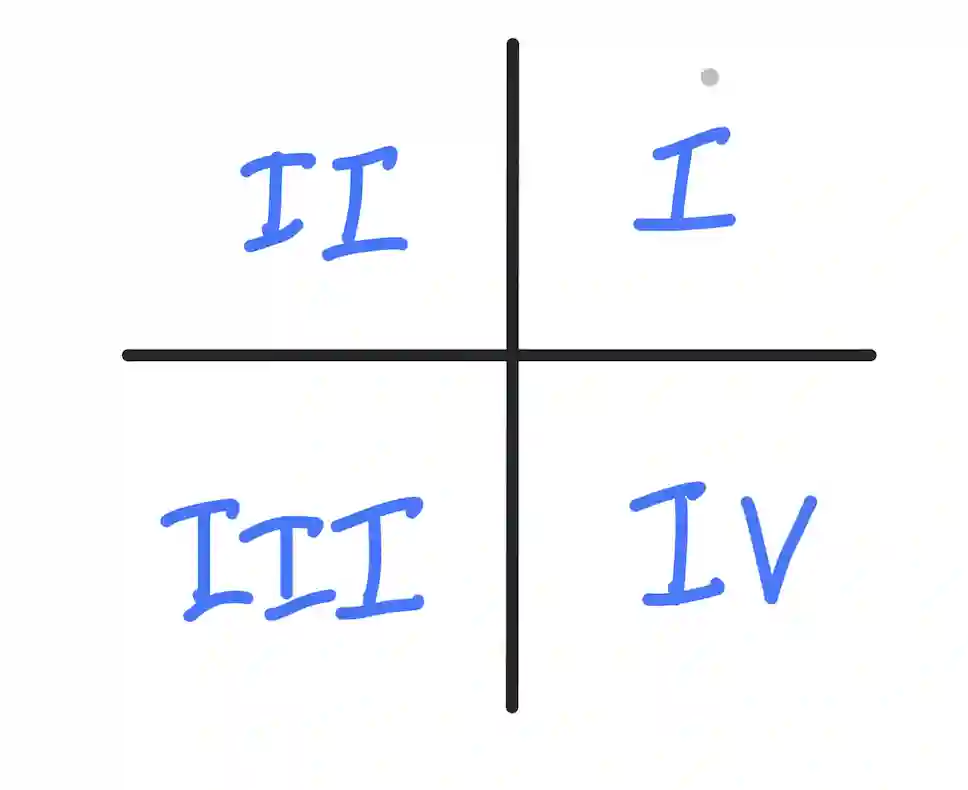
Quadrant I (QI) is located in the upper right-hand corner of the plane, where both x and y have positive values.
Quadrant II (QII) is found in the upper left-hand corner of the plane, with x having negative values and y having positive values.
Quadrant III (QIII) is situated in the bottom left corner, where both x and y have negative values.
Finally, Quadrant IV (QIV) is positioned in the bottom right corner, with x having positive values and y having negative values.
The purpose of labeling quadrants in a coordinate plane is to provide a systematic way of identifying and categorizing points based on their location. By using the labels Quadrant I, Quadrant II, Quadrant III, and Quadrant IV, it becomes easier to refer to specific regions of the coordinate plane.
This labeling scheme allows for quick recognition of the signs of the coordinates and helps in understanding the characteristics and behaviors of points in different parts of the plane. For example, points in Quadrant I have positive x and y values, while points in Quadrant III have negative x and y values.
Below is an example of points plotted.
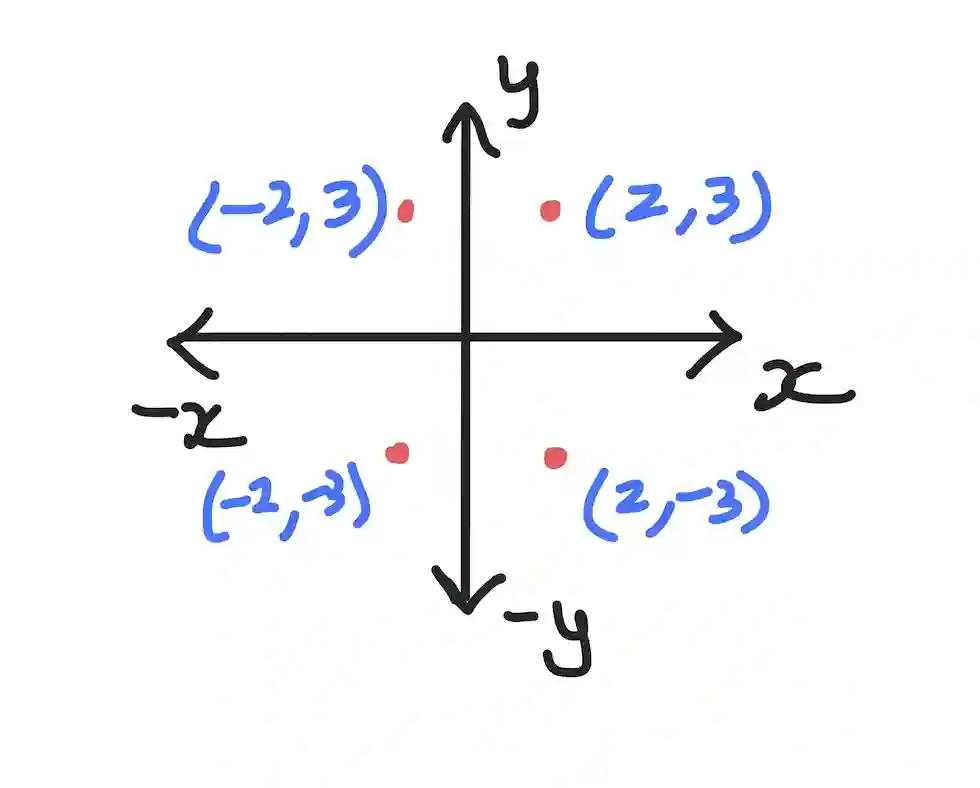
(2,3) has an x-coordinate of 2 and a y-coordinate of 3. Thus this point is in the top-right, or Quadrant I. How do you find this point? You start with the origin, which is point (0,0). Then you move 2 points to the right, and 3 points up.
(-2,3) is the mirror reflection of (2,3) around the y-axis. It has an x-coordinate of -2 and its y-coordinate is unchanged, at 3. This point is in the top-left, or Quadrant II. In this case, you again start with the origin, at point (0,0), move 2 points to the left (since the x-coordinate is negative), and 3 points up.
(-2,-3) is a point that has both x- and y-coordinates negative. Therefore this point is in the bottom-left, or Quadrant III. In this case, you again start with the origin, at point (0,0), move 2 points to the left (since the x-coordinate is still negative), and 3 points down (since the y-coordinate is also negative). This is how you end up in Quadrant III.
Finally, (2,-3) is a point that has only the y-coordinate negative. Therefore this point is in the bottom-right, or Quadrant IV. To reach this point, you again start with the origin, at point (0,0), move 2 points to the right (since the x-coordinate is now positive), and 3 points down (since the y-coordinate is still negative). This is Quadrant IV.
Thus we have come full circle, traveling in a counter-clockwise direction.
What is the takeaway lesson here? If you are given the coordinates of a point, it is easy to determine which coordinate it lies in.
How are quadrants used in real life?
Understanding and using the quadrant labels is essential for various mathematical applications, such as geography and navigation. Below are some examples of how quadrants are used in real-life applications.
In geography, the concept of quadrants is used to specify the location of different places on the Earth's surface. The latitude and longitude lines on maps represent a two-dimensional coordinate system, and the Earth's surface is divided into four quadrants based on the signs of the latitude and longitude coordinates. This system is used for navigation, cartography, and identifying the precise location of geographical features.
In technology, coordinate planes are used in various applications, such as computer graphics, mapping, and GPS systems. For instance, GPS systems use a coordinate plane to determine the exact location of a device on the Earth's surface, and computer graphics applications use coordinate planes to represent and manipulate visual data.
In summary, the labeling of quadrants in a coordinate plane is a fundamental concept that has practical applications in various fields, including mathematics, geography, and technology. Understanding quadrants is essential for identifying the location of points, specifying geographical coordinates, and implementing coordinate-based systems in technology.
If you liked learning about quadrants, learn about consecutive angles!
Want to learn with us? Sign up for 1:1 or small group classes.