Kodeclik Blog
What are Consecutive Angles?
Consecutive angles are a pair of angles that are formed in specific geometric configurations.
To understand what consecutive angles are, you need (1) two parallel lines, and (2) a third line that cuts across these two lines. This third line is called a transversal.
In the below picture, lines l1 and l2 are the parallel lines and t is the transversal.
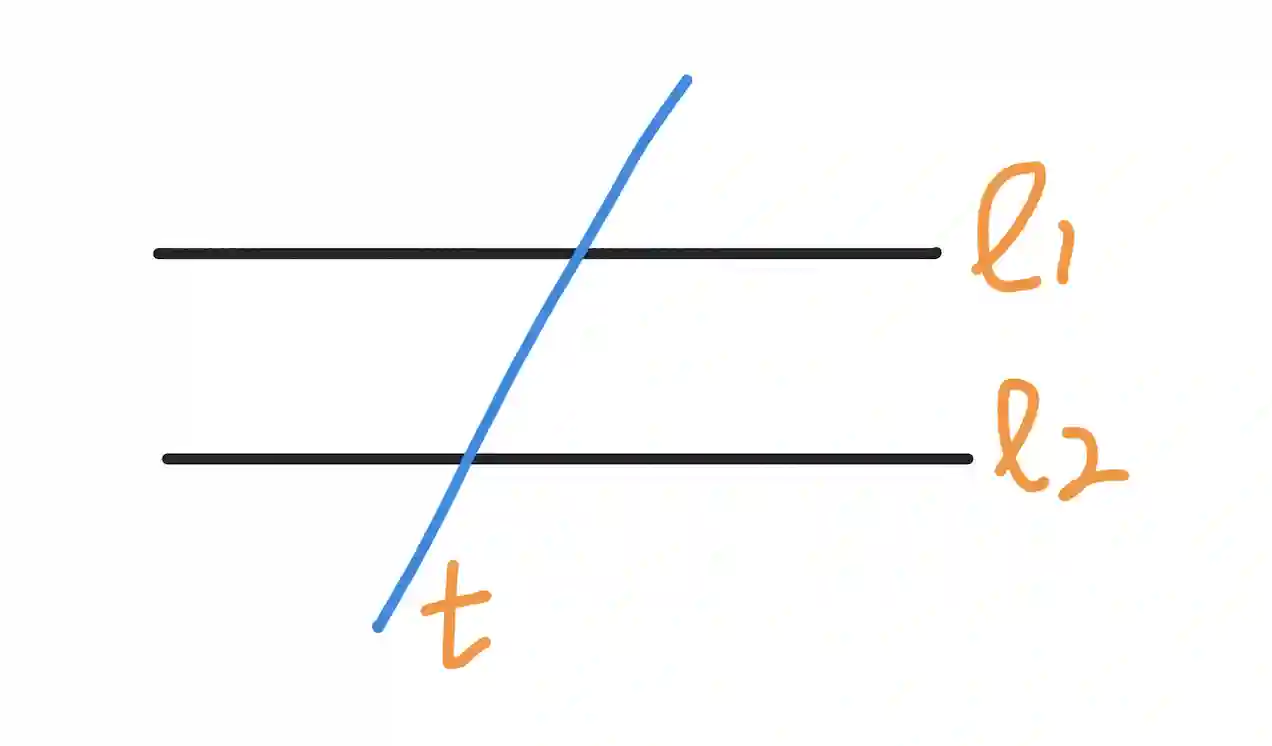
When a transversal intersects two parallel lines, consecutive angles are formed. There are two types of consecutive angles: consecutive interior angles and consecutive exterior angles. Let us look at them in more detail.
Consecutive Interior Angles
Consecutive interior angles are the pair of angles on the same side of the transversal and inside the parallel lines (hence the name interior angles).
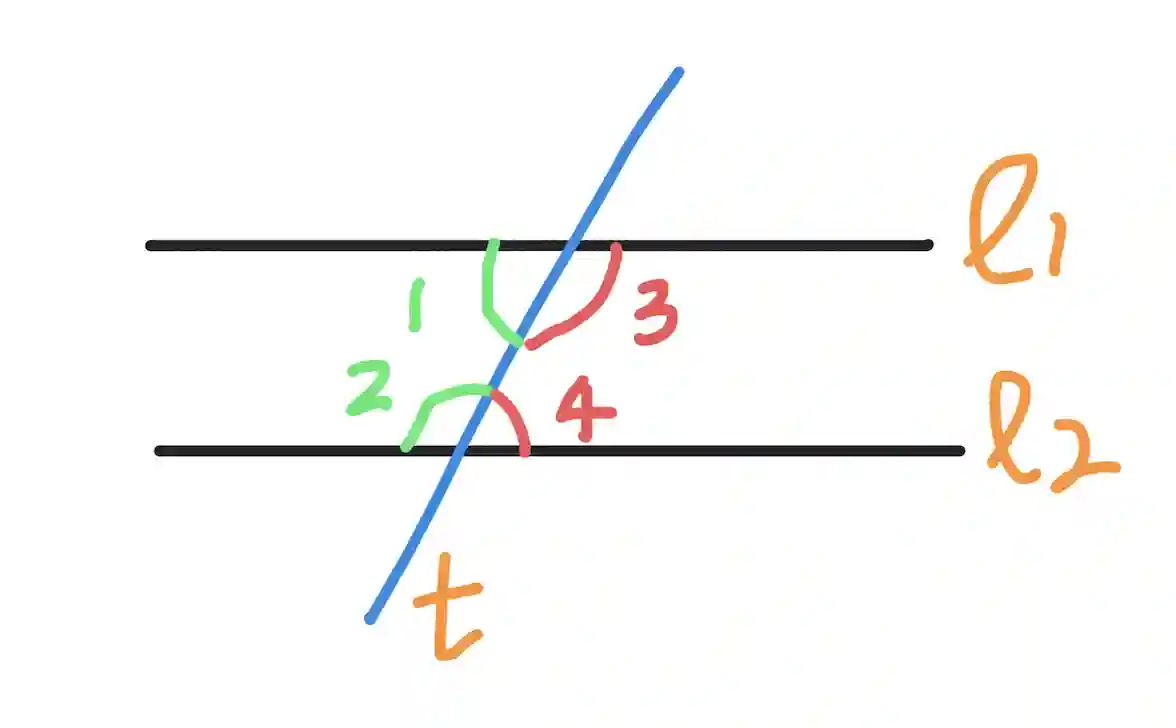
In the above figure, angles 1 and 2 are consecutive interior angles. Similarly, angles 3 and 4 are consecutive interior angles.
Consecutive Interior Angle Theorem
The Consecutive Interior Angle Theorem states that when two parallel lines are intersected by a transversal, the pairs of consecutive interior angles formed on the same side of the transversal are supplementary. This means that their measures add up to 180 degrees.
Visualizing the Theorem
As shown above, imagine two parallel lines intersected by a third line, ie the transversal. Consecutive interior angles are formed on either side of the transversal between the two parallel lines. In the above diagram, angles 1 and 2 are positioned on the same side of the transversal but inside the parallel lines, and are thus consecutive interior angles. Therefore they add upto 180 degrees and are supplementary. Similarly, angles 3 and 4 are supplementary.
Proof of Consecutive Interior Angle Theorem
The proof is quite simple and draws upon the idea of alternate angles. Here is a setp-by-step breakdown of the proof:
Converse of Consecutive Interior Angle Theorem
The converse of the consecutive interior angles theorem states that if a transversal intersects two lines such that a pair of consecutive interior angles are supplementary (i.e., they add up to 180°), then the two lines are parallel.
To break this down further,
Consider the below figure:
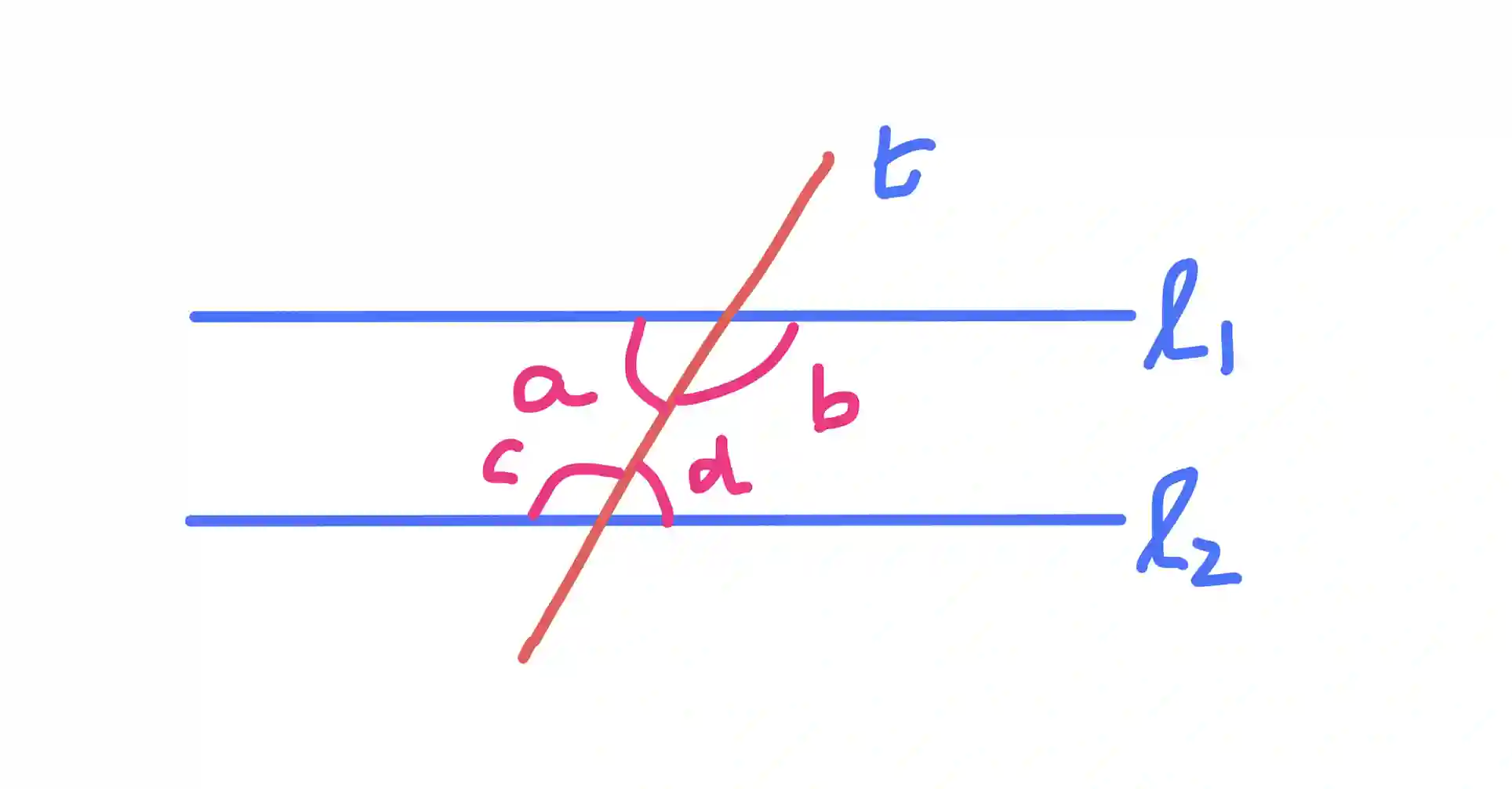
We can prove the converse of the consecutive angles theorem step-by-step as follows:
Therefore, if the consecutive interior angles are supplementary, the lines must be parallel.
This converse theorem is useful in geometry proofs and problem-solving, as it allows us to determine if lines are parallel based on the relationships between angles formed by a transversal.
Example: Find the unknown angles
Consider the below diagram. Only one angle is given (ie 45 degrees). Your task is to find the missing angles.
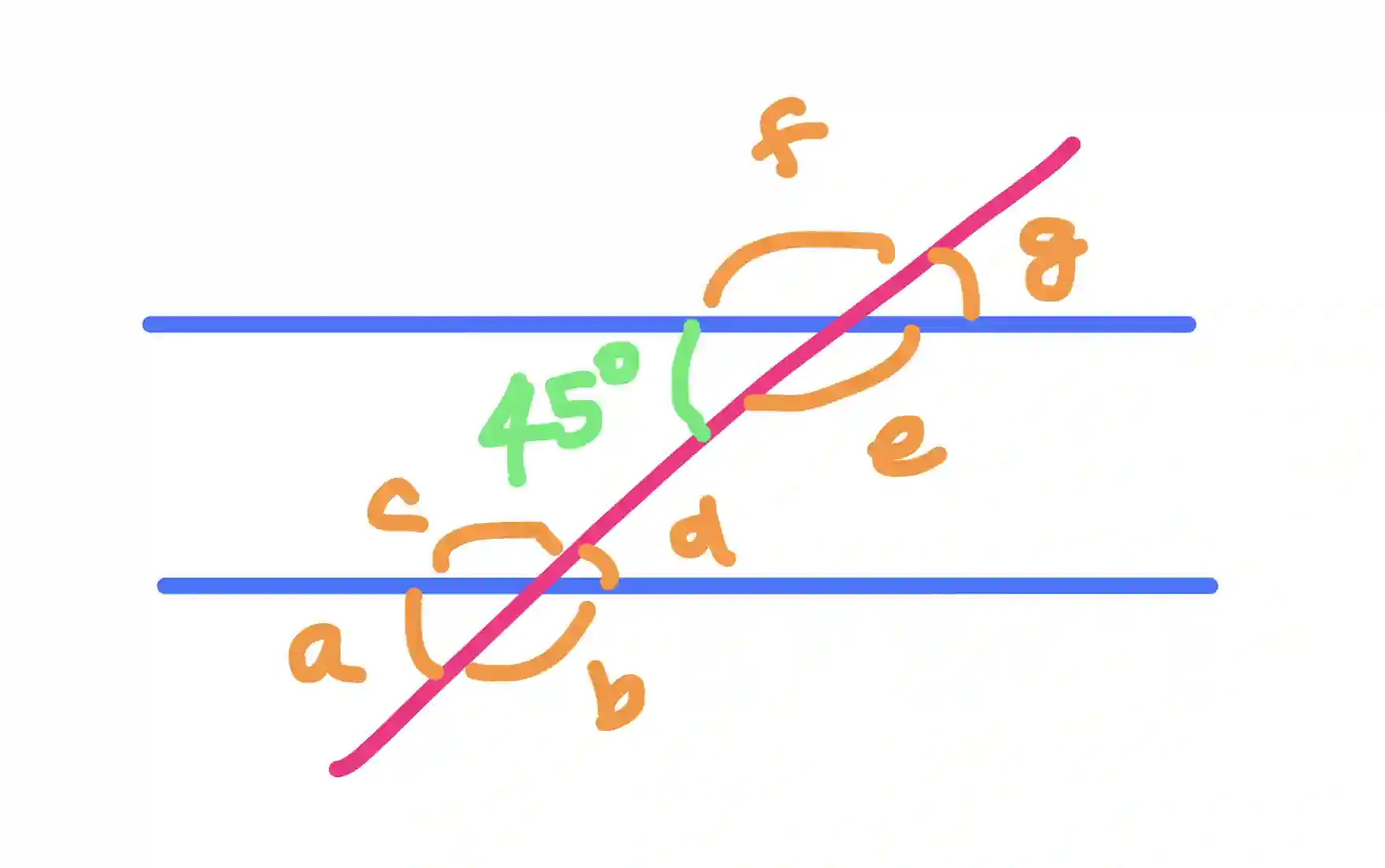
We can proceed step by step as follows:
Thus we have found all angles!
Common Mistakes when using the Consecutive Interior Angles Theorem
When using the consecutive interior angles theorem or its converse, students make several common mistakes:
By being aware of these common mistakes, students can more accurately and effectively apply the consecutive interior angles theorem in geometric proofs and problem-solving.
Applications and Uses of the Consecutive Interior Angles Theorem
The Consecutive Interior Angle Theorem has several practical applications in real-world scenarios. Here are some examples:
Consecutive Exterior Angles
In contrast to consecutive interior angles, consecutive exterior angles are the pair of angles on the same side of the transversal but outside the parallel lines, and it turns out they are also supplementary!
Let us mark consecutive exterior angles in our original diagram. We get:
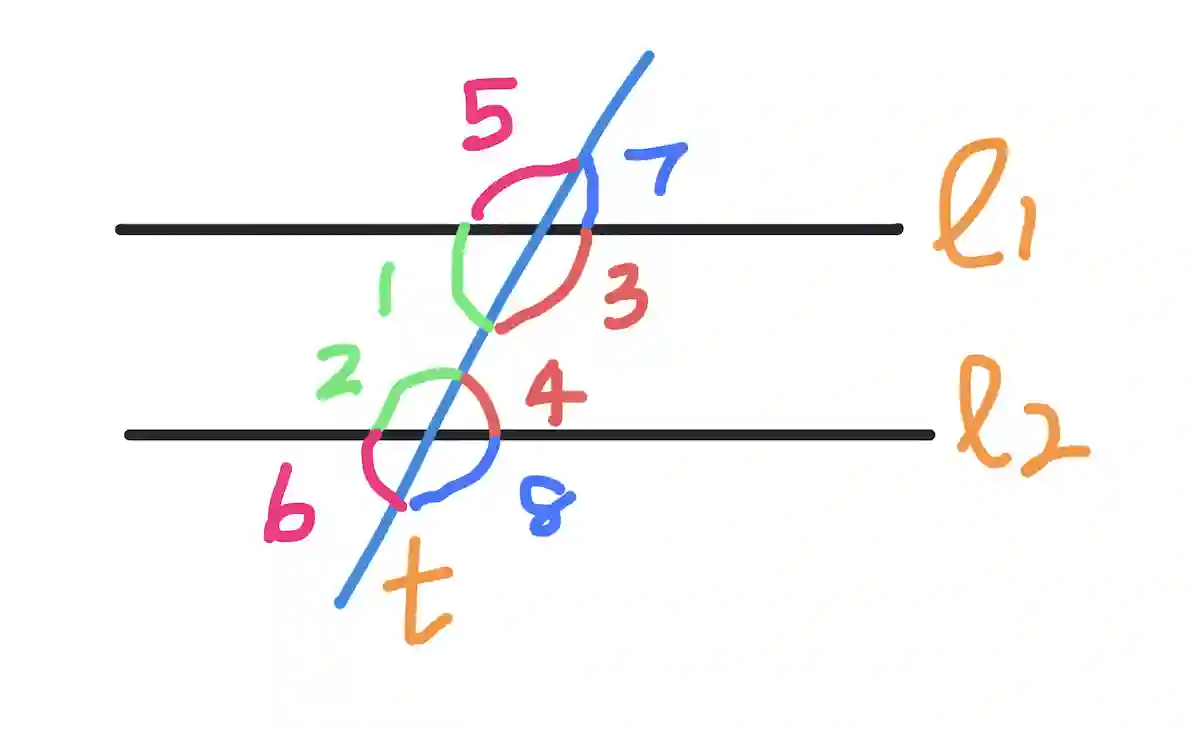
Here, angles 5 and 6 are consecutive exterior angles. Similarly, angles 7 and 8 are consecutive exterior angles. Again, they add up to 180. You can convince yourself that this must be true with a similar idea. Angle 5 is equal to angle 3. Similarly, angle 6 is equal to angle 4. But we already know that angles 3 and 4 are supplementary! (because they are consecutive interior angles!). Thus the consecutive exterior angles 5 and 6 are supplementary. Similarly, consecutive exterior angles 7 and 8 are also supplementary.
Adjacent Angles in a Parallelogram = Consecutive Angles
In a parallelogram, all the adjacent angles are consecutive angles, and their sum is always 180 degrees.
Why are all adjacent angles consecutive? Because in a parallelogram, every side can be viewed as a transversal intersecting two parallel lines, and all the angles of a parallelogram are consecutive angles. Thus, we obtain a picture like this:
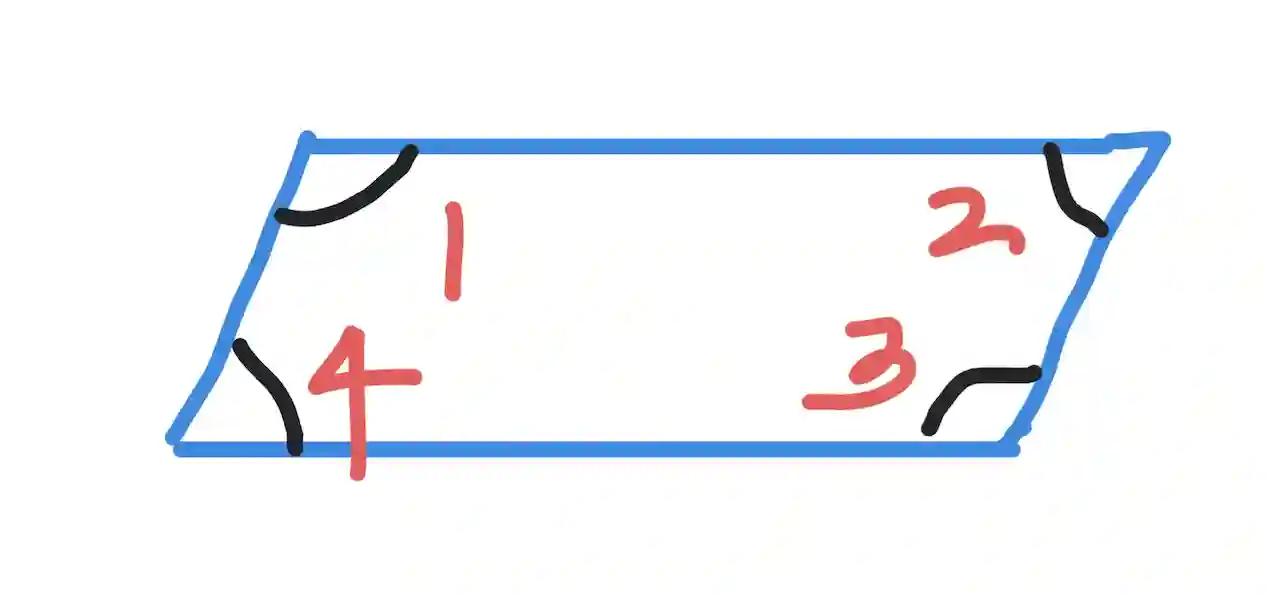
Thus, angles 1 and 2 are supplementary, and so are the pairs (2,3), (3,4), (4,1).
Because adjacent angles in a parallelogram are supplementary, we can verify that all of them add upto 360 degrees.
In general, the sum of the angles in a quadrilateral is always 360 degrees. This is a fundamental property of quadrilaterals, and it holds true for all types of quadrilaterals, regardless of whether they are a parallelogram or not. But in the case of a parallelogram, you also have the additional property that adjacent angles add upto 180 degrees.
For a square or a rectangle, you have an even additional property that all angles are 90 degrees.
For more general quadrilaterals, it is not true that adjacent angles must add upto 180 degrees but all angles must still add upto 360 degrees. For example, if the consecutive angles of a quadrilateral are given in the ratio form of 5:7:11:13, the sum of the angles can be found by using the general formula of 5x + 7x + 11x + 13x = 360, where x is the common factor. By solving for x, the measures of the consecutive angles can be derived. In this specific case, the sum of the consecutive angles is 360 degrees, and the individual angle measures are 50, 70, 110, and 130 degrees, respectively.Note that not all adjacent angle pairs add upto 180 degrees (only two pairs, do, namely 70+110=180, and 130+50=180, but other pairs do not).
Conclusion
To summarize, there are two types of consecutive angles: consecutive interior angles and consecutive exterior angles. Consecutive interior angles are the pair of non-adjacent interior angles that lie on the same side of the transversal, while consecutive exterior angles are the pair of angles on the same side of the transversal and outside the parallel lines. The consecutive interior angles are supplementary, meaning their sum is 180 degrees. The same is true for consecutive exterior angles.
Therefore, consecutive angles are not necessarily equal to each other, but their sum is 180 degrees. This concept is used to solve various problems in geometry and is applicable in real-life scenarios involving parallel lines and transversals
If you liked learning about consecutive angles, learn about quadrants in the 2D plane!
Want to learn with us? Sign up for 1:1 or small group classes.