Kodeclik Blog
How to Make a Random Number Generator in Python
Random numbers are crucial to realism in gaming, machine learning, data science, cryptography, and simulation. Learn all about random numbers and how to generate them in Python.
Why do we need random numbers?
The real world is quite random in nature and to mimic the real world in a computer you need the computer to be able to generate random numbers.
For instance, assume you are playing an arcade-style video game where you have to save the player from enemies or zombies. As the player makes its way through the game, the enemies should surface from random locations in order for the game to be realistic. For this purpose all good gaming programs make use of a random number generator internally.
As a second example, random numbers are important in simulation when you are trying to model real-world phenomena such as clouds, oceans, and forest fires. The randomness element is crucial to ensuring realism in the final simulation.
A final, very important, domain where random numbers are used is in cryptography. Suppose you are worried that your computer’s hard drive might be stolen and that nefarious elements might gain access to your files. One way to prevent this from happening is to encrypt each file in your computer using a key so that even if somebody manages to get hold of the files they will not be able to decipher them without the key. Such a key should be generated by a random number generator and not be an easily guessed passphrase.
Everytime you access a website with the https:// prefix (as opposed to http://) it means that the website is using a secure means of communication (“s” for secure) and is using random numbers to guarantee you that security. As an aside: never do important transactions (e.g., involving credit cards or your personal information) with websites that do not have https in their prefix.
What is really “random” inside a computer?
A computer is made up of a lot of logical elements such as gates, memory units, and processing units, none of which is random. So a basic computer cannot quite generate a truly random number. So how can a computer generate random numbers? The short answer is: it cannot. So how do computers “fake” it? There are broadly two ways. The hardware way to generate random numbers taps into a physical process that is known to be inherently stochastic or not well-understood and uses that process to generate random numbers. Examples of these processes are quantum physics, thermodynamics, beam splitting, and the photoelectric effect. A hardware random number generator uses signals from these processes and converts them to numbers for use in your programs. Today, most computer chips have an on-board random number generator that uses physical phenomena to generate random numbers.
You can create your own rudimentary random number generator by using your phone’s stopwatch. If you switch your stopwatch on, say "Kodeclik" (or some other phrase) and then switch it off, the number of seconds elapsed will be a number that can be considered to be sufficiently random. Below are three tries saying "Kodeclik" and as you can see they generate the numbers: 88, 85, 86. (As the phrase you say becomes longer, it will be extremely difficult to hit upon the same number more than once as they will vary over a larger range.)



A more common way to generate random numbers is to create so-called “pseudo-random numbers”. Pseudo-random means that the numbers are actually generated in a predictable way but for all practical purposes they appear random to the untrained eye. A pseudo-random number begins with an initial number and an algorithm and each time the algorithm is run it generates a new number. Plotting these numbers over time will not reveal any discernable pattern.
How do humans generate random numbers?
Humans are notoriously bad at generating random numbers. Over 8000 students were polled and asked to generate a random number from 0 to 10 and the distribution of results plotted. If people are truly picking numbers at random we should see a uniform distribution of numbers. Instead we see a plot like this:
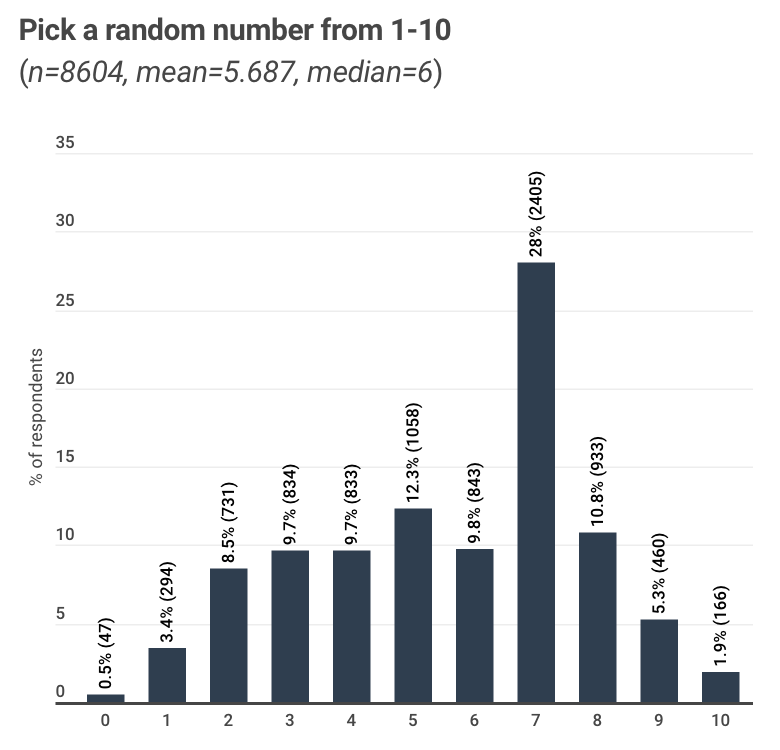
(Figure courtesy Reddit user monkeymaster56
from thread on generating random numbers posted on Reddit channel /r/dataisbeautiful/.)
As you can see 7 is the most commonly picked number, and 0 and 10 are least picked. Perhaps students think numbers like “0”, “5”, “10” are too “obvious” and that they might not look truly random and that “7” is well hidden and thus looks random. Not only that, Prof. Phil Tetlock of the University of Pennsylvania’s Wharton School, believes that humans are also bad at detecting random numbers.
How do you know if a number has been really randomly generated?
We cannot look at a single number and conclude if it is randomly generated. Randomness is a claim of the process generating the number, so you should make the process generate lots of numbers and then plot a distribution of them to see if the results are uniformly distributed. The highest level of randomness (called “entropy”) is when every result is equally likely to be picked. For example if you toss a coin a million times, you should expect heads approximately half a million times and tails approximately half a million times. If they deviate significantly from the expected proportion of 0.5, you can conclude that the coin is not a “fair” one. Similarly, if you throw a die, each side of the die should be equally likely (i.e., happen ⅙ th of the time).
How can we program a random number generator?
Luckily for us, all high-level programming languages today (Python, Java, C, C++) come with libraries that already generate pseudorandom numbers and all we need to do is to call these libraries. We show how to generate a random number in Python below.
Generating a random number in Python
All methods below use the Python random module. This module internally uses what is called the “Mersenne Twister” to generate pseudorandom numbers. So the first step in all programs that follow in this blog post is to “import random” which will give you access to all the random functions in this module. All approaches below involve just a single line of code to generate the random number.
First Method: randint() function
This first method uses the randint() function. The randint() function selects a random integer from a given range. For example the line of code “randint(1,10)” would generate a random integer from 1 to 10 inclusive. To be able to use this function it needs to be written as “random.randint()” as shown in the code below:
import random
number = random.randint(1,10)
print(number) If we run it we will obtain a single number but how do you know it is truly random? Recall that you cannot look at a single run and conclude if it is random. So
let us make a for loop to generate a random integer numerous times. We will also track the average of the generated numbers and you will see that whatever range we use, the average will always be close to the halfway point as we run this, say, 100,000 times! (This still doesn’t prove that it is truly uniformly random; for that purpose you have to count the number of times each number appears and plot a distribution graph like the above.) If we try it like so:
import random
value = 0
tries = 100000
for i in range(tries):
value += random.randint(1,29)
print(value/tries) The last few lines of the output will look something like:
15.0377
15.03771
15.03792
15.03802 Note that 15 is the midpoint of the [1,29] range.
Second Method: randrange() function
Our second method uses the randrange function. The randrange function is the same as the randint function (even the fact that you must use integer values). The key difference between randrange and the randint function is that randrange can take different “steps”. For example the code: “random.randrange(1,30,2)” will generate numbers in steps of two (1,3,5, etc.). Numbers like 2,4, etc. will NOT be generated. As before, lets create a for loop running 1000 times and print the average.
import random
value = 0
tries = 100000
for i in range(tries):
value += random.randrange(1,29)
print(value/tries) Third Method: choice() function
The final method we will be using is the choice function. This function takes an array of elements and chooses from them. For example the code: “random.choice([1,2,3,4])” will choose a random number from 1 to 4. To make a list from one to thirty we will use the code segment: “list(range(1,30))” which creates a list/array with elements from 1 to 30. As usual, we will run this code segment 1000 times to compute the average:
import random
value = 0
tries = 100000
for i in range(tries):
value += random.choice(list(range(1,29)))
print(value/tries) So there you have it - three different ways to generate random integers in Python but recall that they are all pseudorandom numbers, not truly random.
For more math fun, checkout our blog post on generating geometric designs using Desmos. Also learn about other useful Python libraries in our blog post on Top 6 Python Libraries for kids. A good background about algorithms is available in this overview on What is an Algorithm?. Also, see this blog post about Python's enumerate() function. Also learn how to generate a random password in Python.
Want to learn Python with us? Sign up for 1:1 or small group classes.