Kodeclik Blog
How to rotate and scale a vector in Python
Working with vectors in Python can be a tricky process, but it doesn’t have to be. Using the Python math library, you can easily rotate and scale vectors without having to do the math yourself. In this blog post, we’ll explore how to rotate and scale a vector using Python.
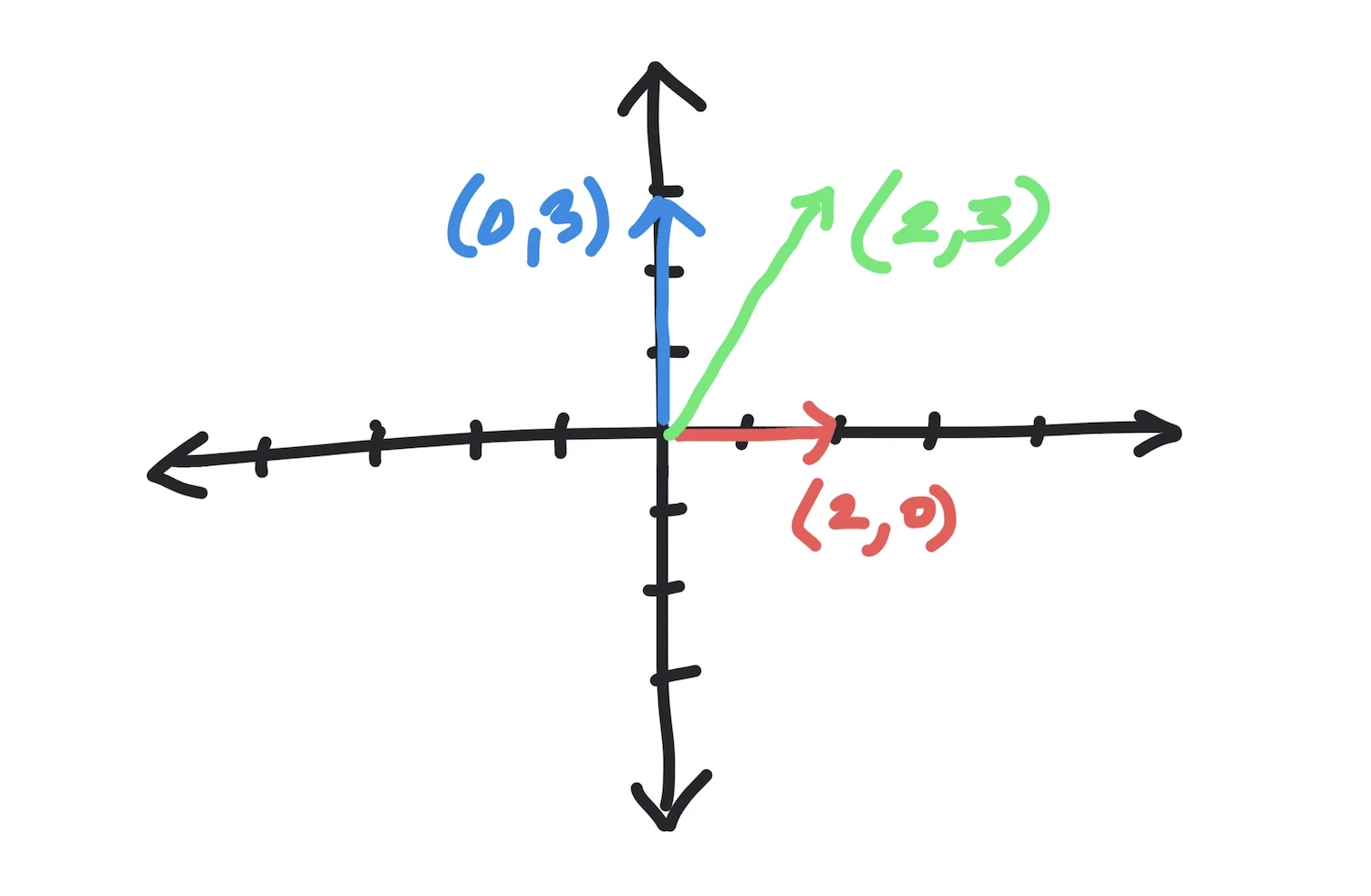
We will focus on 2D vectors, i.e., vectors you can draw and visualize on a flat sheet of paper. For instance the vector (2,0) is along the x-axis, (0,3) is along the y-axis and (2,3) makes progress in both directions. Note that all three vectors start at the origin.
Scaling a vector in Python
Scaling a vector in Python in easy so let us focus on that first. To scale a vector, simply multiply both components of the vector by your scaling factor. For example, if we aim to double the size of our original vector (2,3), we would multiply each side by 2 so that the new vector becomes (4,6). Here is a Python program to represent vectors and scale them:
def scale(coordinates, scale_factor):
(x,y) = coordinates
newx = x*scale_factor
newy = y*scale_factor
return (newx, newy)
p1 = (2,3)
p2 = scale(p1,2)
print(p1)
print(p2)Note that inside the function scale we unpack the coordinates into x and y values, scale each of them by the scale factor, and put them back together into a new vector. The output is:
(2, 3)
(4, 6)as expected.
Rotating a vector in Python
Rotating a vector is more complicated. This requires some understanding of trigonometry. Essentially, we pre-multiply the vector by the rotation matrix. The below figure shows the details of how to do this in matrix notation but fret not the program below shows how to do this with simple equations!
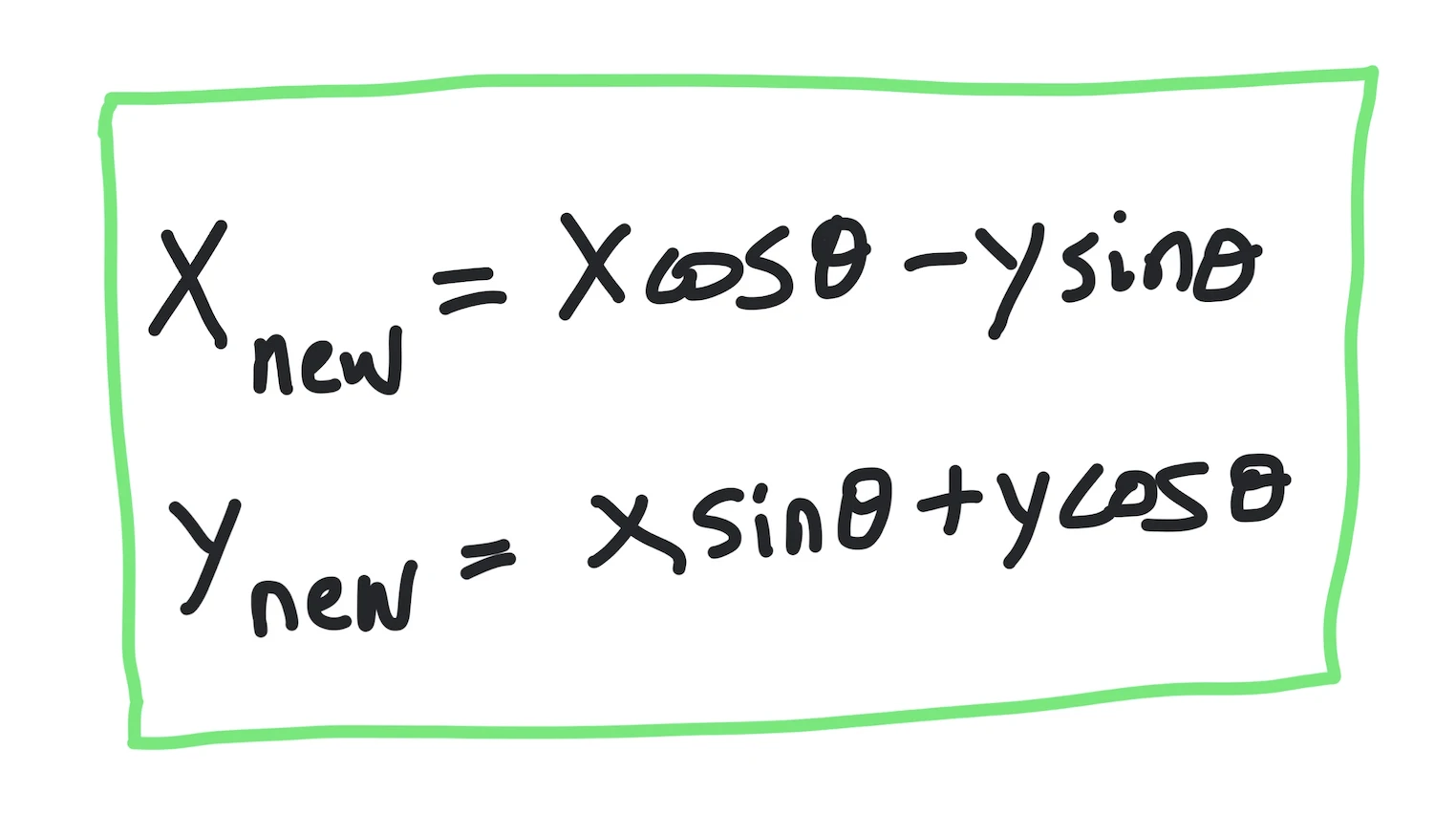
import math as m
def rotate(coordinates, angle):
(x,y) = coordinates
angler = angle*m.pi/180
newx = x*m.cos(angler) - y*m.sin(angler)
newy = x*m.sin(angler) + y*m.cos(angler)
return (newx, newy)
p1 = (2,0)
p2 = (0,3)
p3 = rotate(p1,90)
p4 = rotate(p2,90)
print("Original p1:")
print(p1)
print()
print("Rotated p1:")
print(p3)
print()
print("Original p2:")
print(p2)
print()
print("Rotated p2:")
print(p4)
print()In this program, the rotate function implements the equations above. Not that it takes the input angle in degrees (and converts it to radians internally). After the function is setup, we create two vectors, one along the positive x-axis and one along the positive y-axis. We then rotate both vectors 90 degrees (clockwise). This causes the positive x-axis vector to align with the positive y-axis. Similarly, the positive y-axis vector will align with the negative x-axis.
The output is:
Original p1:
(2, 0)
Rotated p1:
(1.2246467991473532e-16, 2.0)
Original p2:
(0, 3)
Rotated p2:
(-3.0, 1.8369701987210297e-16)The first thing to note is, because of floating point calculations, you get a really small number but not zero. Note that (2,0) has been rotated to (0,2) effectively. Similarly, (0,3) has been rotated to (-3, 0) effectively. Modulo this floating point inconvenience, the above function works admirably.
Scaling and rotating a vector in Python
Because of the way we have written our functions we can easily sequence them one after the other to obtain complex vector manipulations:
import math as m
def rotate(coordinates, angle):
(x,y) = coordinates
angler = angle*m.pi/180
newx = x*m.cos(angler) - y*m.sin(angler)
newy = x*m.sin(angler) + y*m.cos(angler)
return (newx, newy)
def scale(coordinates, scale_factor):
(x,y) = coordinates
newx = x*scale_factor
newy = y*scale_factor
return (newx, newy)
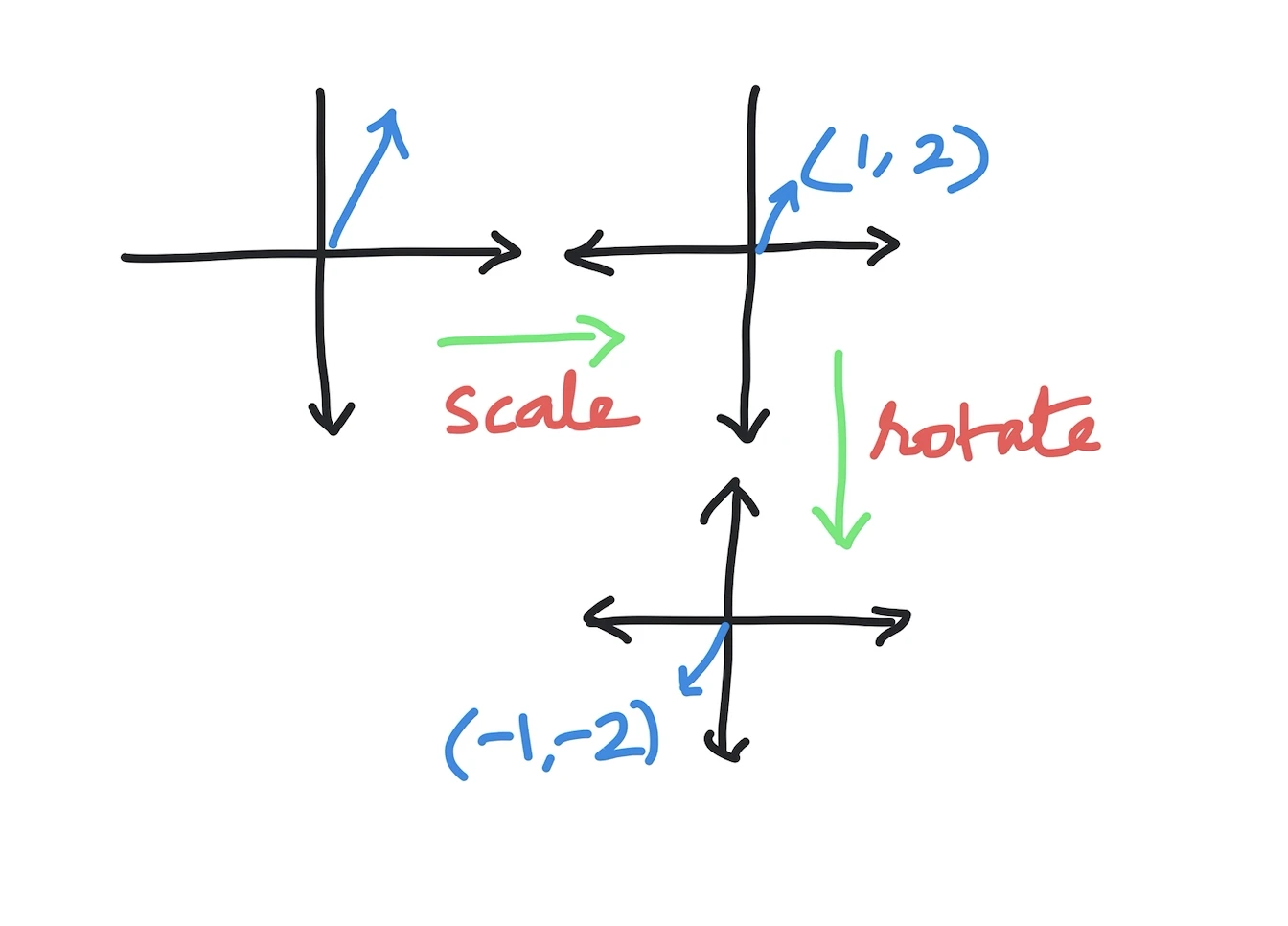
p1 = (2,4)
p1_scaled = scale(p1, 0.5)
p1_scaled_and_rotated = rotate(p1_scaled, 180)
print(p1_scaled_and_rotated)In the above program we begin with vector (2,4). This is then scaled by 0.5, thus giving us (1,2). This vector is then rotated by 180 which means we just take the mirror image of it, giving us (-1,-2). The output is:
(-1.0000000000000002, -1.9999999999999998)Close enough!
In conclusion, rotating and scaling vectors in Python is an important skill that you will find useful in machine learning, computer graphics, or video editing. You can extend these ideas to three dimensions or more.
If you liked this blogpost, learn about the Python numpy.linspace() function.
For more Python content, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.