Kodeclik Blog
How to compute the Manhattan distance in Python numpy
The Manhattan distance is the distance computed in terms of “city blocks” between two locations. In contrast to the Euclidean distance which is measuring the “as the crow flies” distance (by assuming you can directly fly between locations), the Manhattan distance assumes that you can just go horizontally or vertically along city blocks and counts the number of blocks traversed as the distance measure.

The mathematical definition of the Manhattan distance involves taking the absolute value of the differences between respective coordinates and adding them up (as shown in the below figure).
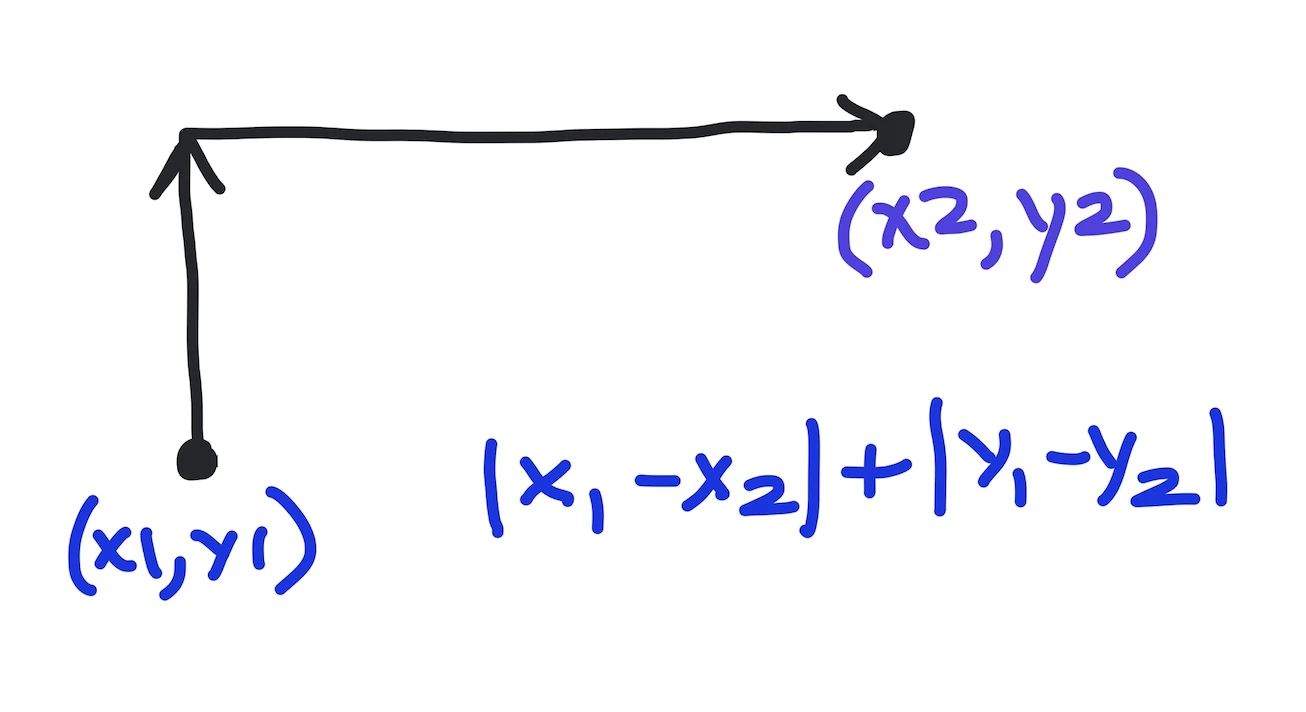
Method 1: Compute Manhattan distance using abs() and sum() functions
Here is a simple way to compute the Manhattan distance. We simply code up the above formula using basic numpy functions, like so:
import numpy as np
location1 = np.array([-1, 1])
location2 = np.array([2, -3])
print("Location 1's coordinates:")
print(location1)
print("Location 2's coordinates:")
print(location2)
print("Manhattan distance between location 1 and location 2:")
print(np.sum(np.abs(location1 - location2)))In the above code, we are first creating two locations at coordinates (-1,1) and (2,-3). Note that the x-coordinates are off by a unit of 3 (i.e., 2 minus -1) and the y-coordinates are off by a unit of 4 (-3 minus 1). The exact signs don’t matter because we are taking the absolute values of these differences and adding them (using np.abs and then np.sum). This returns a single number, a scalar which is the Manhattan distance.
If we run this program, we get:
Location 1's coordinates:
[-1 1]
Location 2's coordinates:
[ 2 -3]
Manhattan Distance between location 1 and location 2:
7This makes sense because the two differences were 3 and 4, and 3 and 4 added up gives you 7.
Method 2: Compute Manhattan distance using the scipy package and cityblock() function
A second way to compute the Manhattan distance is to use the scipy package and the cityblock() function within it. This works as follows:
import numpy as np
from scipy.spatial.distance import cityblock
location1 = np.array([-1, 1])
location2 = np.array([2, -3])
print("Location 1's coordinates:")
print(location1)
print("Location 2's coordinates:")
print(location2)
print("Manhattan distance between location 1 and location 2:")
print(cityblock(location1,location2))Note that in the above code we simply pass location1 and location2 as two arguments to the cityblock() function. The output is the same as before:
Location 1's coordinates:
[-1 1]
Location 2's coordinates:
[ 2 -3]
Manhattan distance between location 1 and location 2:
7We have learnt two different ways to compute the Manhattan distance using the Python numpy module. Which one is your favorite?
Finally, note that we have used points in two dimensional space (like latitude, longitude) and computed distances between them. But the same codes above will work even if your points are in a higher dimensional space, like 3 or higher.
If you liked this blogpost, you should explore a different way to compute distances such as the Euclidean distance.
For more Python content, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.