Kodeclik Blog
How to compute the Euclidean distance in Python numpy
The Euclidean distance is the “crow’s flight” distance or straight line distance between two points. For instance, if you look at the latitude and longitude of two cities, say New York and Boston, the Euclidean distance gives you the length of a rope stretched straight between these two cities.
The mathematical definition of the Euclidean distance involves taking the sum of squared differences between coordinates and then taking the square root of the sum (as shown in the below figure).
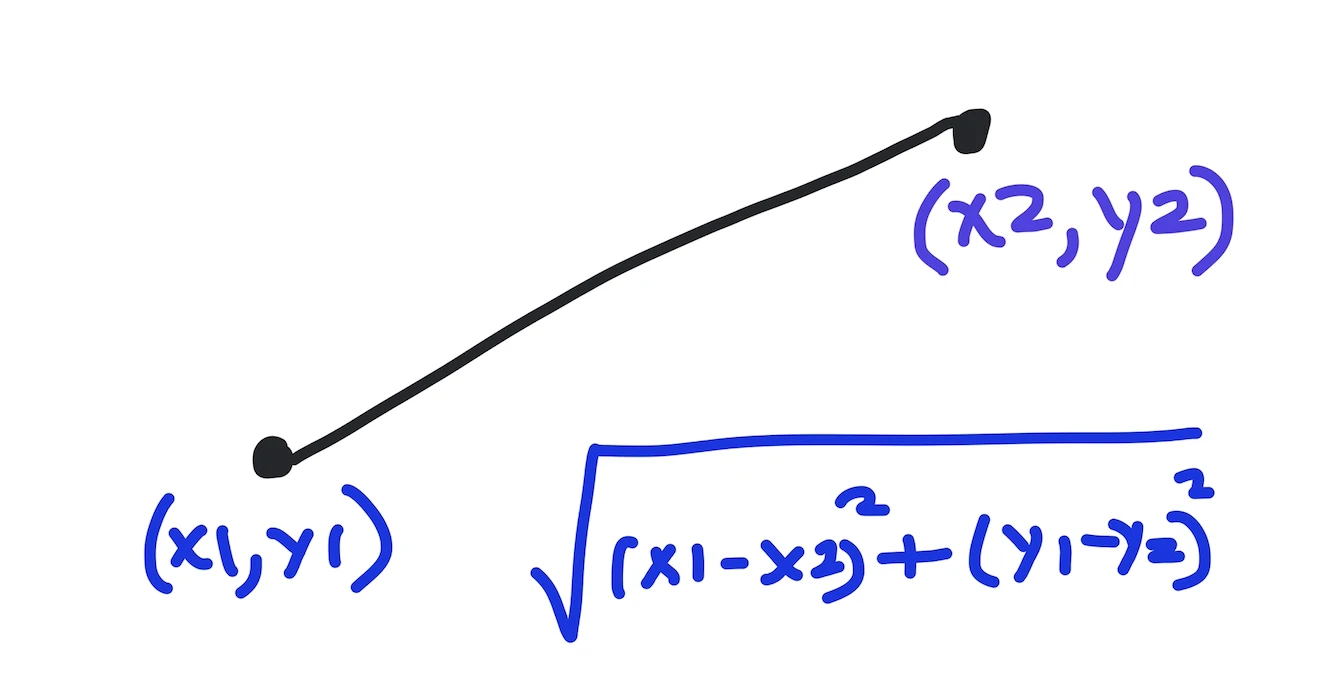
There are three ways to calculate the Euclidean distance using Python numpy. First, we can write the logic of the Euclidean distance in Python using sqrt(), sum(), and square() functions. Second, we can compute the Euclidean distance using dot products with dot(). Third, we can use the np.linalg.norm() function. We will go through these methods one by one.
Method 1: Compute Euclidean distance using sqrt(), sum(), and square() functions
Here is a simple way to compute the Euclidean distance. We simply code up the above formula using basic numpy functions, like so:
import numpy as np
location1 = np.array([-1,1])
location2 = np.array([2,-3])
print("Location 1's coordinates:")
print(location1)
print("Location 2's coordinates:")
print(location2)
print("Distance between location 1 and location 2:")
print(np.sqrt(np.sum(np.square(location1 - location2))))In the above code, we are first creating two locations at coordinates (-1,1) and (2,-3). (These are just for example and in reality you can plugin actual latitude and longitude coordinates of your favorite cities.) Note that the x-coordinates are off by a unit of 3 (i.e., 2 minus -1) and the y-coordinates are off by a unit of 4 (-3 minus 1). The exact signs don’t matter because we are squaring these differences and adding them (using np.square and then np.sum). This returns a single number, a scalar which is then used in the square root function to return the Euclidean distance.
If we run this program, we get:
Location 1's coordinates:
[-1 1]
Location 2's coordinates:
[ 2 -3]
Distance between location 1 and location 2:
5.0This makes sense because the two differences where 3 and 4, and 3 and 4 are the two non-hypotenuse sides of a right angled triangle with 5 as the value of the hypotenuse, which is what is returned.
Method 2: Compute Euclidean distance using dot() and sqrt()
A second way to compute the Euclidean distance is to use the property that the Euclidean distance is basically the square of the dot product of the difference between the two points (as vectors) with itself. This works as follows:
import numpy as np
location1 = np.array([-1,1])
location2 = np.array([2,-3])
print("Location 1's coordinates:")
print(location1)
print("Location 2's coordinates:")
print(location2)
print("Distance between location 1 and location 2:")
print(np.sqrt(np.dot(location1-location2,location1-location2)))Note that in the above code it is very important to first compute (location1-location) which for our example is (-3,4). When we do a dot product of (-3,4) with itself, we get: -3*-3 + 4*4 = 9+16 = 25. Finally we take the square root of it, to obtain 5. The output is the same as before:
Location 1's coordinates:
[-1 1]
Location 2's coordinates:
[ 2 -3]
Distance between location 1 and location 2:
5.0Method 3: Compute Euclidean distance using the linalg.norm() function
The final approach to compute the Euclidean distance is the easiest and it uses the built-in function called linalg.norm() within the numpy module. Here is how that works:
import numpy as np
location1 = np.array([-1,1])
location2 = np.array([2,-3])
print("Location 1's coordinates:")
print(location1)
print("Location 2's coordinates:")
print(location2)
print("Distance between location 1 and location 2:")
print(np.linalg.norm(location1-location2))Note that we compute the difference between the two locations as usual and pass it to the linalg.norm() function within numpy and it directly does the computation for us to yield the distance:
Location 1's coordinates:
[-1 1]
Location 2's coordinates:
[ 2 -3]
Distance between location 1 and location 2:
5.0We have seen three different ways to compute the Euclidean distance using the Python numpy module. Which one is your favorite?
Finally, note that we have used points in two dimensional space (like latitude, longitude) and computed distances between them. But the same codes above will work even if your points are in a higher dimensional space, like 3 or higher.
If you liked this blogpost, you should explore a different way to compute distances such as the Manhattan distance.
For more Python content, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.