Kodeclik Blog
Computing the nth row of Pascal’s Triangle
Pascal’s triangle is a very useful construct in discrete mathematics. It is a way to organize binomial coefficients, or different ways of choosing “k” elements from “n” elements.
Below is an example of the first few rows of Pascal’s triangle:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1After the first two rows, each element is formed by adding the two numbers immediately above it (to the left and to the right) in the previous row, as shown below.
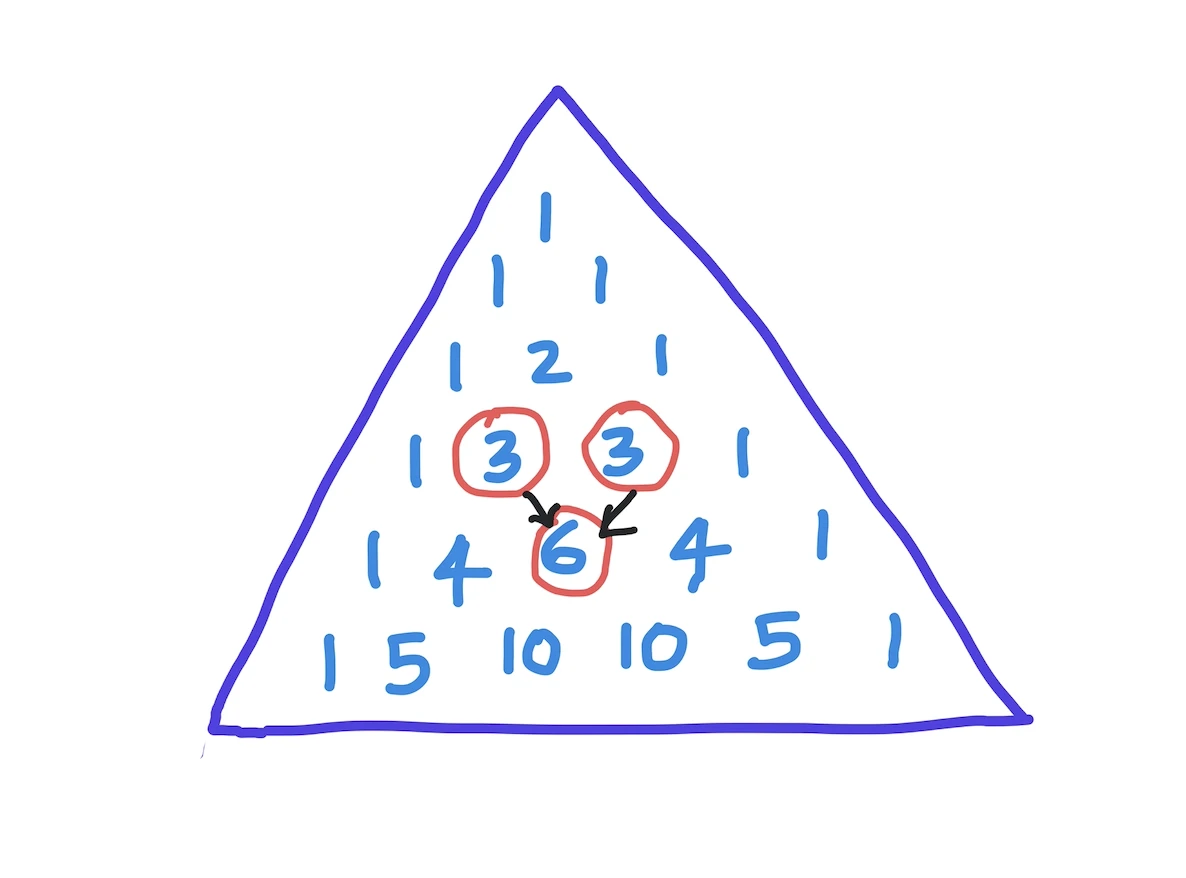
For ease of exposition we will print them like this:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1The nth element of row k is formed by adding the (n-1)th and nth elements of row (k-1). Also, from a combinatorial perspective, the nth element of row k gives the number of ways of choosing k-1 elements from n-1 elements.
To confirm this, let us take the 5th row which begins “1 4”. This should give you an indication that we are choosing from 4 elements. Let us consider choosing 2 elements from these 4 elements, so we are looking at the third element of the fifth row. In other words, to choose k elements from n elements, we look at the (n+1)th row and look at the (k+1)th element.
Let us assume these four elements are a,b,c,d. Since we are choosing two elements from the four element set, the combinations are:
ab
ac
ad
bc
bd
cdThus, there are 6 combinations which is what the (fifth row, third element) reveals. Let us now focus on printing the Pascal’s triangle. We will consider three ways.
Method 1: Use the math.factorial() function
The math package comes with a readymade factorial() function that can be used to calculate the combinations. The number of ways of choosing k elements from n elements is (n!) divided by k! (n-k)!. Here is code to do precisely this:
from math import factorial
def nck(n,k):
return(factorial(n)/(factorial(k)*factorial(n-k)))
print(nck(4,2))The output is:
6.0You can notice that the output is being printed in decimal format and you can use the int() function to print it in integer format:
from math import factorial
def nck(n,k):
return(factorial(n)/(factorial(k)*factorial(n-k)))
print(int(nck(4,2)))The output will now be:
6Now using this function we can print Pascal’s triangle by simply computing the binomial coefficients and printing them:
for i in range(7):
for j in range(i+1):
print(int(nck(i,j)),' ',end='')
print()In the above code we are printing the first 7 rows. The outer iteration begins from 0 to 6. The inner loop prints each row by beginning from 1 and going till the outer iteration index. Inside the loop, we use the nck() function we have written earlier. The end=’’ part ensures that the coefficients in a single row are printed without going to a newline. Once a row is printed we issue a blank print statement to move to the next line. The output will be:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1Method 2: Use iteration
Our second approach does not rely on the Math.factorial() function. Instead we generate each row by using the previous element just printed and scaling it suitably. Below is the code to generate the same number of rows of Pascal’s triangle as above:
print(1)
for i in range(6):
num = 1
for j in range(i+1):
print(num,' ',end='')
num = num * (i -j +1)//(j+1)
print(1)In the above code, we first print the single row containing the singleton element “1” using a lone print statement. Then we print one row at a time. For each row, we initialize the first element (in variable num) to 1. Then we enter a nested for loop to print the requisite number of entries. Each subsequent number is the previous number scaled by a suitable value (because “n choose k” is a scaled version of “n choose k-1”).
The output is, as before:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1Method 3: Use recursion
In recursion we go back to the original property of Pascal’s triangle, which is that each number is the sum of two numbers above it. To this end we write a simple recursive function to encapsulate this idea:
def generate_element(row,col):
if (col==1 or row==col):
return(1)
else:
return(generate_element(row-1,col)
+generate_element(row-1,col-1))
for i in range(7):
for j in range(i+1):
print(generate_element(i+1,j+1),' ',end='')
print()In the above code, the generate_element() function is written recursively. It prints a “1” for the first and last element (the base case of the recursion) and calls itself recursively for all other elements. The output will be, as expected:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1As simple and elegant as the above code is, it is not a very efficient way of computing Pascal’s triangle. This is because in order to compute an element, we recursively compute smaller elements and keep doing this for every new element. We will end up calling the function generate_element() over and over again for the same inputs numerous times. This extra work will not appear much when we print only a few rows, as done here but will add up significantly. One sollution to overcome this drawback is to store the values as they are generated so that we don’t call it recursively (left as an exercise for you!)
If you liked this blogpost, see our blogpost on arrays vs lists in Python. Also see a more in-depth coverage of the math.comb() function that directly helps calculate the number of combinations.
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.
