Kodeclik Blog

Python math.comb()

Let us suppose you received 4 candies from your Halloween trick or treating, e.g., “Kit Kat”, “Snickers”, “Reeses”, and “Crackle”. You are allowed to choose two from this set of 4 candies. How many ways can you do so? Here are the ways:

“Kit Kat”, “Snickers”
“Kit Kat”, “Reeses”
“Kit Kat”, “Crackle”
“Snickers”, “Reeses”
“Snickers”, “Crackle”
“Reeses”, “Crackle”

Note that the order in which you choose them does not matter, so “Kit Kat”, “Snickers” is the same as “Snickers”, “Kit Kat” (which is not listed).

It is easy enough to list the combinations for this small case but what if you had 20 types of candies and you need to choose 5 of them. How can we count the combinations systematically without worrying that you have missed some combination? There is a Python math function for that!

The Python math.comb() function takes two arguments “n” and “k” and returns the number of ways in which k elements can be chosen from a set of n elements. Note that k can be at most n. We read this as “n choose k”. The mathematical formula for “n choose k” is n! / (n-k)!, i.e., it is a ratio of two factorials.

Here is a simple Python program mimicking our candy scenario:

import math as m

candies = 4
allowed = 2
print(m.comb(candies, allowed))

The output will be:

In fact, we can try to see how many different ways there are in choosing different numbers of elements from our set of 4 candies. In other words, we keep n fixed at 4 and vary k from 0 to 4. There is only 1 way to choose 0 elements from 4 (i.e., not choose anything at all). There is also only 1 way to choose 4 elements from 4 (i.e., choose all of them). In between values of k (i.e., 1, 2, and 3) will give intermediate values. Here is a simple program to explore this using a for loop:

import math as m

candies = 4
allowed = 2

for items in range(candies+1):
  print(m.comb(candies,items))

The output is:

Thus, there are 4 ways (see second line) to choose 1 candy from the set of all candies (we choose them individually). There are 6 ways to choose 2 candies (what we have seen). Finally, there are 4 ways to choose 3 candies (this is easy to see because if we are choosing 3 candies, we are discarding one of them, and there are 4 ways to discard one).

Here is a program that provides more descriptive output:

import math as m

candies = 4
allowed = 2

for items in range(candies+1):
  print("There are " + 
        str(m.comb(candies,items)) +
        " ways to choose " +
        str(items) + " items from " +
        str(candies) + " candies.")

The output is:

There are 1 ways to choose 0 items from 4 candies.
There are 4 ways to choose 1 items from 4 candies.
There are 6 ways to choose 2 items from 4 candies.
There are 4 ways to choose 3 items from 4 candies.
There are 1 ways to choose 4 items from 4 candies.

If you are with us so far you can extend this program to multiple numbers of candies and for each number, exploring all the different ways to choose a given number of candies:

import math as m

candies = 12
for items in range(candies+1):
  for r in range(items+1):
    print(m.comb(items,r),end=' ')
  print()

In the above program we are varying both n and k in the math.comb() invocation. This gives us a beautiful pattern:

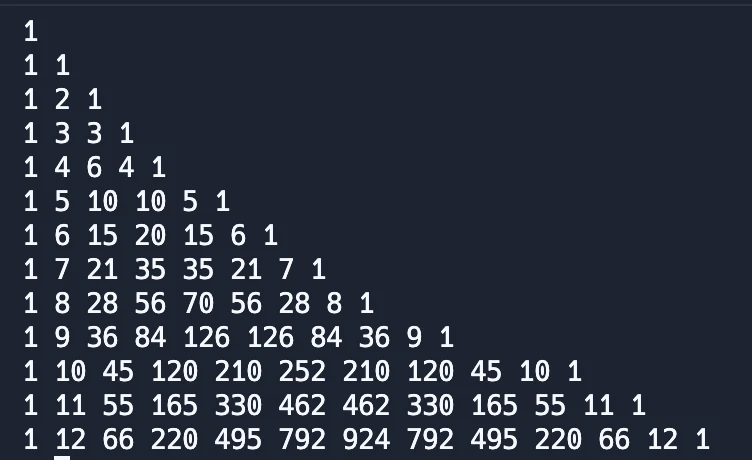
$Python math.comb() function$

1 
1 1 
1 2 1 
1 3 3 1 
1 4 6 4 1 
1 5 10 10 5 1 
1 6 15 20 15 6 1 
1 7 21 35 35 21 7 1 
1 8 28 56 70 56 28 8 1 
1 9 36 84 126 126 84 36 9 1 
1 10 45 120 210 252 210 120 45 10 1 
1 11 55 165 330 462 462 330 165 55 11 1 
1 12 66 220 495 792 924 792 495 220 66 12 1

This is also known as Pascal’s triangle which is usually center-aligned (but you get the idea).

To summarize, the math.comb() function from Python’s math module calculates the number of combinations possible in choosing k items from a total of n items. See also our blogpost on computing the nth row of Pascal's triangle in Python.

For more Python content, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!

Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!

Want to learn Python with us? Sign up for 1:1 or small group classes.

Python math.comb()

Join our mailing list