Kodeclik Blog
math.cos() in Python
Recall that the cosine of an angle is defined as the adjacent side (adjacent to the angle) divided by the hypotenuse in a right-angled triangle. It is well known that the cosine of zero is 1 and the cosine of 90 degrees (which is pi/2 radians) is 0. The math.cos() is a handy function in Python to compute these trigonometric ratios.
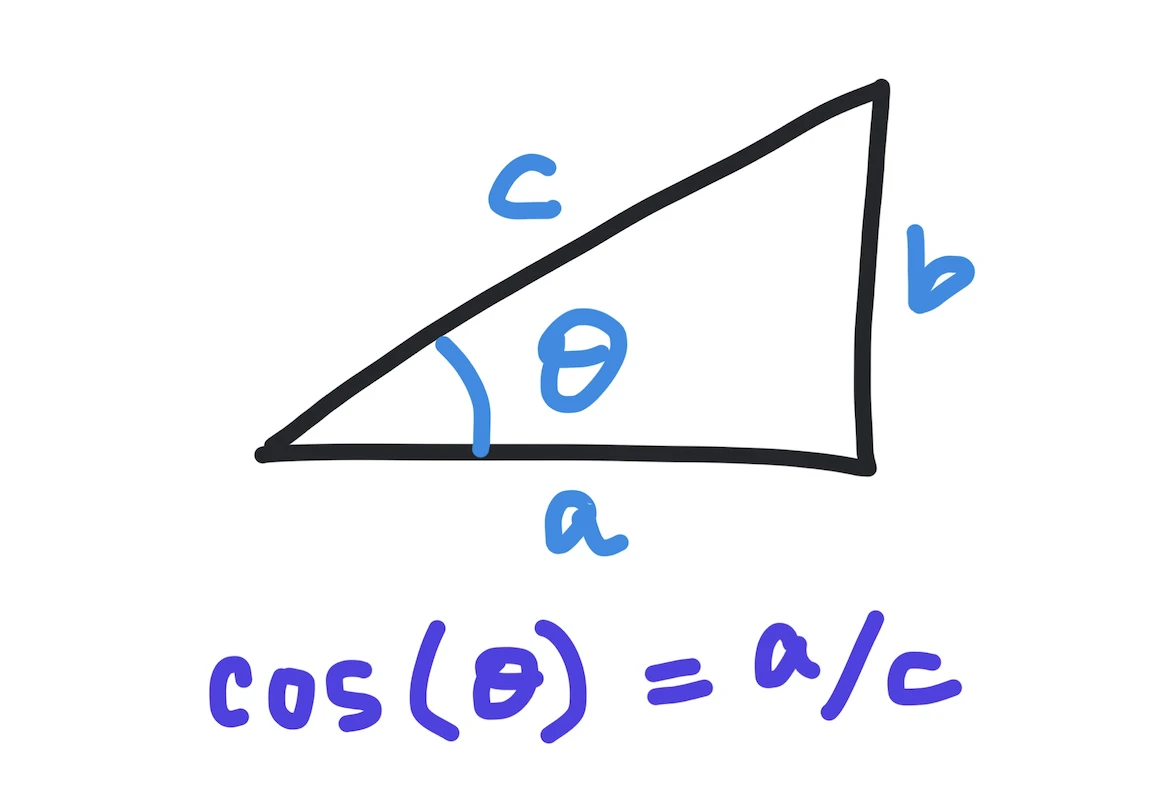
Consider the following program:
import math
print("Cosine of " + str(0) +
" degrees is " + str(math.cos(0)))
print("Cosine of " + str(90) +
" degrees is " + str(math.cos(90*math.pi/180)))Note that in the second line we are careful to convert degrees to radians (by scaling by pi/180) before passing the result to the cos() function. (In the first line, we know that 0 degrees is the same as 0 radians, so we do not need to be so careful.)
The output is:
Cosine of 0 degrees is 1.0
Cosine of 90 degrees is 6.123233995736766e-17The second line’s output shows floating point errors in the math module, i.e., the output is a number quite close to zero but not exactly zero.
Computing the cosine function using Taylor series approximation
If you did not have access to the cos() function you can approximate the cos function by using a Taylor series expansion (expanded around 0) as shown in the below function:
import math
def cosine_approx(theta, n):
# first convert theta degrees to radians
t = theta * math.pi / 180
sum = 0
# now use a series
for i in range(0, n):
sum = sum + math.pow(-1, i) *
math.pow(t, 2 * i) / math.factorial(2 * i)
return (sum)The above function takes two inputs, viz. theta, the angle for which we wish to compute the cosine and n, the number of terms. Inside the function, we first convert the angle to radians and then use a for loop to add up terms according to the Taylor expansion for cos(theta). Even though the Taylor’s series is infinite, we are approximating it here with a finite number of terms.
Now we can use this function like so:
print("Cosine of " + str(0) + " degrees is "
+ str(math.cos(0)))
print("Cosine of " + str(90) + " degrees is "
+ str(math.cos(90*math.pi/180)))
print("Cosine of " + str(90) + " degrees is "
+ str(cosine_approx(90,15)))The output will be:
Cosine of 0 degrees is 1.0
Cosine of 90 degrees is 6.123233995736766e-17
Cosine of 90 degrees is 4.25394673467242e-17As you can see we are using 15 terms in the cosine function expansion to approximate the value of cos(). And you can see that the result is not exactly 0.0 (just like the case of the Math.cos() function). If we increase the number of terms we will get increasingly more accurate results. Here is some code to explore this:
import math
def cosine_approx(theta, n):
# first convert theta degrees to radians
t = theta * math.pi / 180
sum = 0
# now use a series
for i in range(0, n):
sum = sum + math.pow(-1, i) *
math.pow(t, 2 * i) / math.factorial(2 * i)
return (sum)
print("Taylor series computation of cos(x)")
for k in range(1,25):
print("Cosine of " + str(90) + " degrees, with "
+ str(k) + " terms is " + str(cosine_approx(90,k)))The output will be:
Taylor series computation of cos(x)
Cosine of 90 degrees, with 1 terms is 1.0
Cosine of 90 degrees, with 2 terms is -0.23370055013616975
Cosine of 90 degrees, with 3 terms is 0.019968957764878226
Cosine of 90 degrees, with 4 terms is -0.0008945229984747317
Cosine of 90 degrees, with 5 terms is 2.473727636469452e-05
Cosine of 90 degrees, with 6 terms is -4.6476600836607633e-07
Cosine of 90 degrees, with 7 terms is 6.321469515740575e-09
Cosine of 90 degrees, with 8 terms is -6.513356805127347e-11
Cosine of 90 degrees, with 9 terms is 5.260630985212103e-13
Cosine of 90 degrees, with 10 terms is -3.3769215522516056e-15
Cosine of 90 degrees, with 11 terms is 6.08176268469988e-17
Cosine of 90 degrees, with 12 terms is 4.245771032544636e-17
Cosine of 90 degrees, with 13 terms is 4.253977785846482e-17
Cosine of 90 degrees, with 14 terms is 4.253946632997056e-17
Cosine of 90 degrees, with 15 terms is 4.25394673467242e-17
Cosine of 90 degrees, with 16 terms is 4.253946734384059e-17
Cosine of 90 degrees, with 17 terms is 4.2539467343847764e-17
Cosine of 90 degrees, with 18 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 19 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 20 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 21 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 22 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 23 terms is 4.2539467343847745e-17
Cosine of 90 degrees, with 24 terms is 4.2539467343847745e-17As you can see, after a few terms we see the series converging to the desired value.
In conclusion, you can use the math.cos() function which is a built-in function in the Math module of Python or you can construct your own approximation using Taylor series.
If you liked learning about the math.cos() function, you should checkout our blogposts on the math.sin() and math.tan() functions!
Now that you have mastered the math.cos() function, checkout the math.ceil() and math.floor() functions! Also
learn about the math domain error in Python and how to fix it!
Interested in more things Python? Checkout our post on Python queues. Also see our blogpost on Python's enumerate() capability. Also if you like Python+math content, see our blogpost on Magic Squares. Finally, master the Python print function!
Want to learn Python with us? Sign up for 1:1 or small group classes.