Kodeclik Blog

How to draw a Sierpinski Triangle in Python

The Sierpinski Triangle is a fascinating fractal pattern that forms an equilateral triangle subdivided recursively into smaller equilateral triangles.

The pattern is named after the Polish mathematician Wacław Sierpiński who formally described it in 1915, but it is believed to have appeared centuries earlier as decorative patterns. (As an aside Sierpiński was a prolific mathematician who published over 700 papers and 50 books, contributing significantly to set theory, number theory, and topology. The triangle bearing his name represents just one of his many mathematical contributions, though it has become perhaps his most visually recognizable legacy.)

The Sierpinski Triangle design can also be found in 13th-century Cosmati mosaics in the Anagni Cathedral, Italy, medieval Roman church decorations, Various architectural elements and mandalas throughout central Italy.

How to construct a Sierpinski Triangle

The triangle is created through a simple recursive process:

1. Start with an equilateral triangle
2. Connect the midpoints of each side to create four smaller triangles
3. Remove the center triangle
4. Repeat this process infinitely with the remaining triangles.

Here is an example of a Sierpinski triangle:

Why is the Sierpinski triangle interesting?

The Sierpinski Triangle exhibits several remarkable characteristics. For instance, its area approaches zero as iterations continue to infinity but It has an infinite perimeter. It is a self-similar fractal, meaning the pattern repeats identically at any magnification.

Relationship between the Sierpinski triangle and Pascal’s triangle

The Sierpinski Triangle emerges naturally within Pascal's Triangle through a fascinating mathematical connection. See the below figure courtesy of the Fractal Foundation.

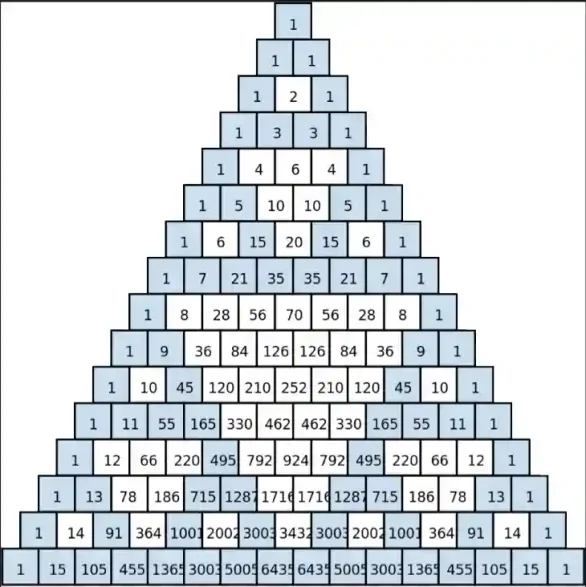
When you color all the odd numbers in Pascal's Triangle, the resulting pattern forms the Sierpinski Triangle fractal. This pattern becomes clearer as you extend Pascal's Triangle to more rows, with each odd number represented as 1 and each even number as 0.

This connection between Pascal's Triangle and the Sierpinski Triangle demonstrates how complex fractal patterns can emerge from simple arithmetic rules, making it a powerful educational tool for understanding both number patterns and fractal geometry.

How can we program the Sierpinski triangle in Python?

To program (ie draw) the Sierpinksi triangle we need to mimic the recursive procedure above in your Python program. We also need to do it using python turtle, a module that supports turtle graphics.

Python's turtle graphics is a beginner-friendly way to create drawings by controlling a virtual "turtle" that moves around the screen leaving a trail behind it. The coordinate system in turtle graphics places the origin (0,0) at the center of the window, with the x-axis extending positively to the right and the y-axis extending positively upward.

Drawing the Sierpinski triangle of order 0

Here is a basic Python program to draw the Sierpinski triangle of order 0 (ie just one triangle).

import turtle

# Create and setup the turtle
screen = turtle.Screen()
screen.bgcolor("white")
t = turtle.Turtle()
t.speed(0)  # Fastest speed
t.color("green")

# Move to starting position
t.penup()
t.goto(-200, -150)  # Starting from bottom left
t.pendown()

# Draw a single triangle
side_length = 400
for _ in range(3):
    t.forward(side_length)
    t.left(120)  # Turn 120 degrees for equilateral triangle

# Hide the turtle cursor
t.hideturtle()

# Keep the window open until clicked
screen.exitonclick()

The program above positions the turtle at (-200, -150), which is below and to the left of the center of the screen. The turtle's movement is controlled by two primary commands: 'forward()' which moves in the current direction, and 'left()' which rotates counterclockwise by a specified number of degrees. In turtle graphics, angles work like a compass: 0 degrees points east, 90 degrees points north, 180 degrees points west, and 270 degrees points south.

The program creates an equilateral triangle by repeating a simple pattern three times: move forward by 400 pixels, then turn left by 120 degrees. The 120-degree turns are used because an equilateral triangle has three equal angles of 60 degrees each, and to maintain the same direction when drawing the next side, the turtle needs to turn the supplementary angle (180° - 60° = 120°). The program finishes by hiding the turtle cursor with hideturtle() and waiting for a click to close with exitonclick().

The output will be:

Drawing the Sierpinski triangle of higher orders

We will now attempt to draw Sierpinski triangles using recursive programming techniques again using Python’s turtle library.

Let us write a main function 'draw_sierpinski' that takes three parameters: a turtle object (t), the order of recursion (determining the complexity of the pattern), and the size of the current triangle. When order is 0, it draws a simple filled triangle, which serves as the base case for the recursion. For any higher order, it recursively draws three smaller triangles, each with half the size of the current triangle.

import turtle

def draw_sierpinski(t, order, size):
    if order == 0:
        # Draw a filled triangle
        t.begin_fill()
        for _ in range(3):
            t.forward(size)
            t.left(120)
        t.end_fill()
    else:
        # Recursively draw three smaller triangles
        for _ in range(3):
            draw_sierpinski(t, order-1, size/2)
            t.forward(size)
            t.left(120)

def setup_turtle():
    # Initialize and configure the turtle
    screen = turtle.Screen()
    screen.bgcolor("white")
    t = turtle.Turtle()
    t.hideturtle()
    t.speed(0)  # Fastest speed
    t.color("green")
    t.penup()

    # Position turtle to start drawing from bottom left
    t.goto(-200, -150)
    t.pendown()
    return t, screen

def main():
    # Get the order from user
    order = int(input("Enter the order of Sierpinski Triangle (0-6 recommended): "))

    # Setup turtle
    t, screen = setup_turtle()

    # Draw the triangle
    draw_sierpinski(t, order, 400)

    # Keep the window open until clicked
    screen.exitonclick()

if __name__ == "__main__":
    main()

The recursion works by following a specific pattern: at each step, it draws a triangle of order n-1 (half the current size), moves forward by the current size, turns left 120 degrees, and repeats this process three times. This creates the characteristic pattern where each triangle is composed of three smaller triangles, with the middle space left empty. For example, a level 2 triangle will first create three level 1 triangles, and each level 1 triangle will create three level 0 (filled) triangles.

The setup_turtle() function handles all the initial configuration, creating a white background, setting the turtle's speed to maximum, and positioning it at (-200, -150) to ensure the drawing is centered in the window. The main() function ties everything together by getting user input for the order (recommending 0-6 to keep processing time reasonable), setting up the turtle, and initiating the drawing process. The program uses the if name == "main": idiom to ensure the main() function only runs when the script is executed directly.

When run, the program demonstrates how simple recursive rules can create complex fractal patterns. Each increase in order doubles the detail of the pattern, with order 0 producing a single filled triangle, order 1 producing three triangles, order 2 producing nine triangles, and so on. The pattern continues with each order containing three times as many triangles as the previous order, creating the distinctive self-similar fractal.

For order 1, the output will be:

For order 2, the output will be:

For order 3, the output will be:

And so on. You get the idea!

We will leave it as an exercise for you to determine what order the figure at the top of this blogpost uses. Enjoy!

Enjoy this blogpost? Want to learn Python with us? Sign up for 1:1 or small group classes.